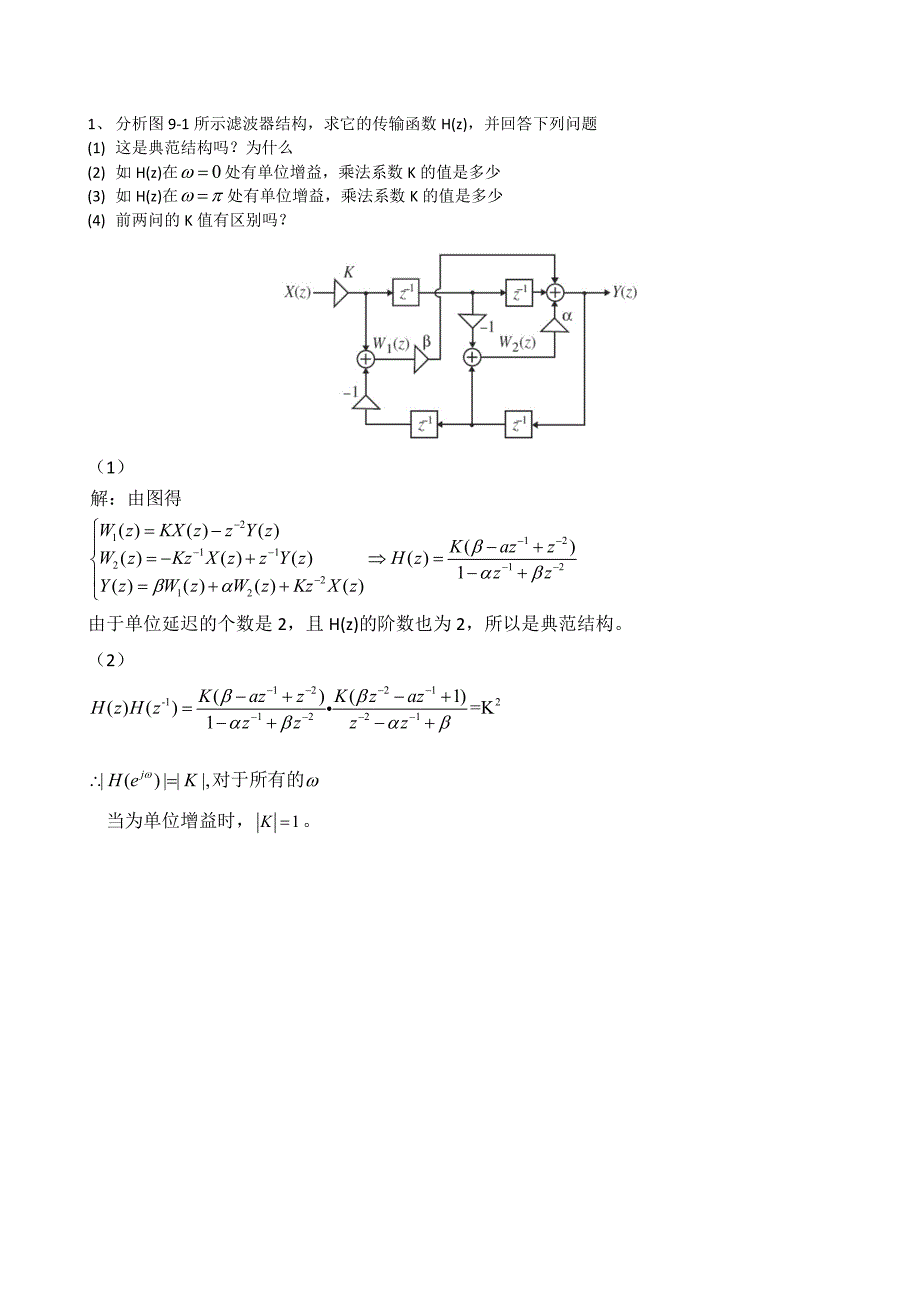
1 分析图 9 1 所示滤波器结构 求它的传输函数 H z 并回答下列问题 1 这是典范结构吗 为什么 2 如 H z 在0 处有单位增益 乘法系数 K 的值是多少 3 如 H z 在 处有单位增益 乘法系数 K 的值是多少 4 前两问的 K 值有区别吗 1 2 1 12 11 2 12 2 12 1 W zKX zz Y z Kazz W zKz X zz Y zH z zz Y zW zW zKzX z 解 由图得 由于单位延迟的个数是 2 且 H z 的阶数也为 2 所以是典范结构 2 1221 12 1221 1 K 1 j KazzKzaz H z H z zzzz H eK 对于所有的 当为单位增益时 1K 2 分析图所示的滤波器结构 其中所有乘法器的系数均是实数 求它的传输函数 H z 若滤 波器是 BIBO 稳定的 乘法器的系数值的范围是什么 解 由图可知 由上可得 1 1 若要系统稳定 则其极点需要全部落在单位圆内 即 1 and 1 1 3 4 已知 FIR 系统的传输函数如下 画出以下形式的实现框图 1 两种不同的直接类型 2 6 个一阶系统级联 3 3 个 2 阶系统级联 4 4 个 3 阶系统级联 5 2 个 1 阶和 2 个 2 阶系统级联 解 1 123456 1 3 65 44 321 9440 4660 0467H zzzzzzz 型和直接型转置结构两种 2 111111 1 0 6 1 0 6 1 0 6 1 0 6 1 0 6 1 0 6 H zzzzzzz 3 121212 1 1 20 36 1 1 20 36 1 1 20 36 H zzzzzzz 系统的传输函数如下 画出以下形式的实现框图 1 0 6 H zz 阶系统级联 123456 1 3 65 44 321 9440 4660 0467H zzzzzzz 111111 1 0 6 1 0 6 1 0 6 1 0 6 1 0 6 1 0 6 H zzzzzzz 121212 1 1 20 36 1 1 20 36 1 1 20 36 H zzzzzzz 1 6 1 0 6 H zz 123456 1 3 65 44 321 9440 4660 0467 其结构可采用直接 111111 1 0 6 1 0 6 1 0 6 1 0 6 1 0 6 1 0 6 4 123123 1 1 81 080 216 1 1 81 080 216 H zzzzzzz 5 111212 1 0 6 1 0 6 1 1 20 36 1 1 20 36 zzzzzz 5 1 4 分支多相的公式为 则 0 4 8 1 5 9 2 6 3 7 实现结果如下图所示 Z 1Z 1 4 Z 1Z 1 4 Z 1 Z 1 Z 1 h h 3 3 h h 2 2 h h 1 1 h h 0 0 h h 7 7 h h 6 6 h h 9 9 h h 5 5 h h 8 8 h h 4 4 y n y n x n x n 2 3 分支多相的公式为 则 0 3 6 9 1 4 7 2 5 8 Z 1 Z 1 h h 4 4 h h 2 2 h h 1 1 h h 0 0 h h 7 7 h h 6 6 h h 9 9 h h 5 5 h h 8 8 h h 3 3 y n y n x n x n Z 3Z 3Z 3 2 2 分支多相的公式为 则 0 2 4 6 8 1 3 5 7 9 Z 1 h h 4 4 h h 2 2 h h 1 1 h h 0 0 h h 7 7 h h 6 6 h h 9 9 h h 5 5 h h 8 8 h h 3 3 y n y n x n x n Z 2Z 2Z 2Z 2 6 7 设计一个长度为 8 的 4 型线性相位 FIR 的最少乘法器结构 8 证明分子分母均为 3 阶实系数的多项式的 IIR 滤波器有 36 种不同的级联实现方案 证 因为是 IIR 滤波器 所以滤波器的传递函数公式可以表示为 因为分子和分母都是 3 阶的多项式 所以分子和分母都可以通过因式分解 分解为 3 个相乘 的因子 其中分母的 3 个因式表示为 D1 z D2 z D3 z 分子的 3 个因式表示为 P1 z P 2 z P 3 z 由于要求是级联实现方案 该 IIR 滤波器可以表示为 3 个一阶 IIR 滤波器相乘的形 势 可以为 也可以为 分子分母不同的排列组合有 3 2 36 种 所以有 36 种不同的级联实现方案 9 10 已知下列因果 IIR 系统的传输函数 求两种不同级联典范实现结构 1 2 1 1 2 1 2 2 0 2z0 6z 32 4z 1 23 2z4 2z 1 0 75z z6 2z 4 5 30 5 2 20 3 0 2 0 5z 0 1 H z zz H z zzz 1 7 解 1 直接型结构 1 2 1 1 2 1 z3z1 0 8z 0 3 1 1 6z2 1z1 0 75z H z 直接型转置结构 1 2 1 1 2 1 z0 8z1 3z 0 3 1 1 6z2 1z1 0 75z H z 2 直接型结构 1 1 2 1 1 1 2 3 1 0 85z1 4 5z30 5z 1 0 15z1 0 2z1 0 5z0 1z H z 直接型转置 1 1 2 1 1 1 2 1 4 5z3 1 0 85z30 5z 1 0 15z1 0 2z1 0 5z0 1z H z 11 解 1 0 2 0 6 3 2 4 2 3 2 4 2 1 0 75 0 6 0 48 1 8 1 44 2 1 5 3 2 2 4 4 2 3 15 0 6 1 32 1 44 2 4 7 6 6 3 15 I 型并联可以表示为 1 0 75 2 2 2 3 2 4 2 1 0 75 1 1 6 2 1 2 4 7 6 6 3 15 2 3 2 4 2 0 75 0 75 2 2 4 7 3 2 0 75 6 6 4 2 0 75 3 15 所以 2 2 0 4 7 3 2 0 75 0 6 6 6 4 2 0 75 1 32 3 15 1 44 16 35 2 39 554 1365 6742 6825 Z 1 B B 0 750 75 Z 1 C C 1 61 6 Z 1 D D 2 1 2 1 A A XYXY II 型并联可以表示为 1 0 75 2 2 2 3 2 4 2 1 0 75 1 1 6 2 1 Z 1 B B 0 750 75 Z 1 C C1 61 6 Z 1 D D 2 1 2 1 A A X X Y Y 2 1 7 6 2 4 5 3 0 5 2 0 3 0 2 0 5 0 1 1 7 6 2 4 5 3 0 5 2 0 1 0 06 0 5 0 1 I 型并联可以表示为 1 0 05 0 03 1 0 5 0 1 Z 1 D D 0 5 0 5 Z 1 E E 0 1 0 1 A A X X Y Y Z 1 B B 0 05 0 05 Z 1 C C 0 030 03 II 型并联可以表示为 1 0 05 0 03 1 0 5 0 1 Z 1 C C 0 5 0 5 Z 1 E E 0 1 0 1 A A X X Y Y Z 1 B B 0 05 0 05 Z 1 D D 0 030 03 13 已知一个因果 LTI 离散时间系统对输入 0 2 n x nu n 的输出为 1 0 4 0 3 0 4 1 nn y nu nu n 1 确定系统的传输函数 2 确定系统的差分方程 3 用不多于 3 个乘法器给出这个系统的典范直接型实现结构 4 给出系统的并联 I 型实现结构 5 给出整个系统的冲激响应闭合式 解 1 1 1 1 1 1 1 10 3z1 0 3z1 1 0 4z1 0 4z1 0 4z1 0 2z Y zX z 1 1 1 2 1 1 1 0 3z 1 0 2z 1 0 5z0 06z 1 0 4z1 0 4z Y z H z X z 20 510 0620 41y nx nx nx ny n 3 1 0 125 0 15 1 0 4z 1 4 H z 0 875z 0 15 0 125 0 4 n nu n 5 h n 0 875 n 1 6 因为 11 111 10 410 4 10 310 310 3 zz X z zzz 所以 111 1 11 10 3 10 2 10 4 10 2 10 410 3 zzz Y zH z X zz zz 0 2 1 y nnn 9 14 解 由图可得出系统传递函数为 1 5 1 1 1 0 2 由已知的传递函数可知 4 5 6 0 2 0 08 12 1 0 4 8 1 0 2 8 1 5 1 0 4 1 1 0 2 对比两个公式 可以得出 A 8 B 0 4 15 1 111212 1 46 0 24 12 5 10 4 1 10 80 6 33 H zzzzzzz 2 111112 2 0 24 1 1 1 1 4024 10 71306 1 1 3488 Hzzzzzzz 16 4 阶 IIR 的传输函数 用 MATLAB 完成以下问题 1 2 3 4 1 2 3 4 0 35490 2002z0 7031z0 2002z0 3549z 1 1 2522z1 9448z0 9774z0 5595z H z 1 以因式形式表示 H z 2 两种典范级联结构 3 实现并联 I 和并联 II 典范结构 解 1 1 2 1 2 1 2 1 2 0 3549 1 0 5958zz 1 0 03169zz 1 0 6209z0 9845z 1 0 6313z0 5681z H z 2 传递函数可表示为 1 2 1 2 1 2 1 2 0 3549 1 0 5958zz 1 0 03169zz 1 0 6209z0 9845z 1 0 6313z0 5681z H z 和 1 2 1 2 1 2 1 2 0 3549 1 0 03169zz 1 0 5958zz 1 0 6209z0 9845z 1 0 6313z0 5681z H z 下面是两种结构类型 3 1 1 1 2 1 2 0 01330 0094z0 2661 0 4299z 0 6343 1 0 6209z0 9845z1 0 6313z0 5681z H z