资源预览内容
space
第1页 / 共122页
space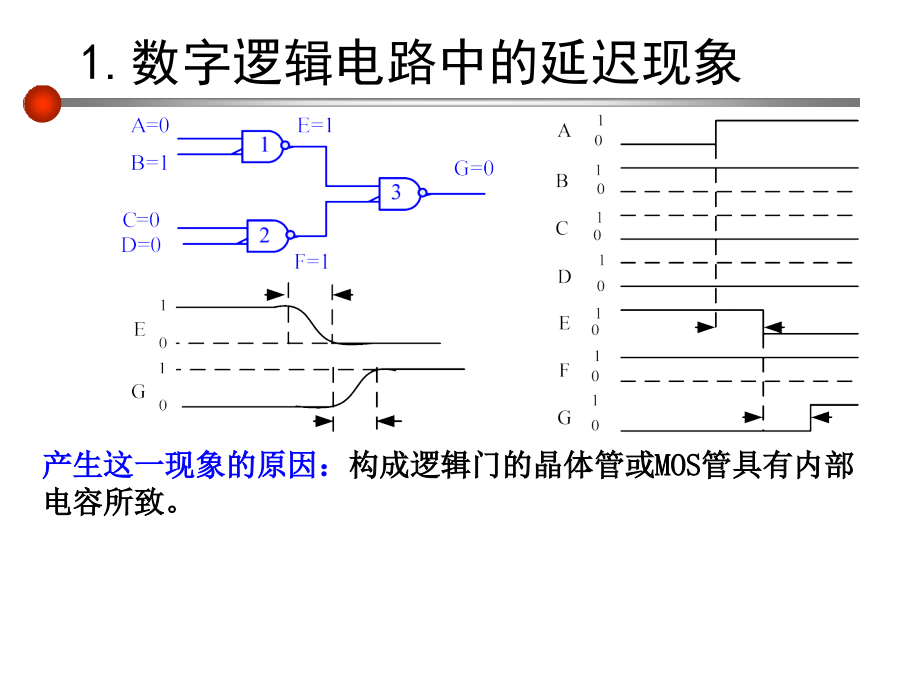
第2页 / 共122页
space
第3页 / 共122页
space
第4页 / 共122页
space
第5页 / 共122页
space
第6页 / 共122页
space
第7页 / 共122页
space
第8页 / 共122页
space
第9页 / 共122页
space
第10页 / 共122页
亲,该文档总共122页,到这儿已超出免费预览范围,如果喜欢就下载吧!
资源描述
5-1 电容元件,1.数字逻辑电路中的延迟现象,产生这一现象的原因:构成逻辑门的晶体管或MOS管具有内部电容所致。,2.电容器(capacitor),绝缘介质,电容器是一种能够存储电荷乃至电场能量的器件。,理想电容器应该只具有存储电荷从而在电容器中建立电场的作用,因而是一种电荷与电压相约束的器件。,充电,3.电容元件,电容元件是实际电容器的理想化模型。,2.1 定义:如果在任一时刻t,一个二端元件的端电压u(t)与其存储的电荷q(t)之间的关系可以用u-q平面上的一条曲线确定,则称此二端元件为电容元件。,2.2 符号,3.电容元件,2.3 线性非时变电容元件:电容元件的特性曲线是u-q平面上的一条过原点的直线,且不随时间而变化。,即:,2.4 电容(capacitance):C,单位:法拉(F)V,C,微法( ),皮法(pF),或:,电容的VCR,在关联参考方向下:,非关联参考方向:,通常,电压、电流采用关联参考方向。,结论:某一时刻,电容的电流取决于该时刻电容电压的变化率。,电容的动态特性,电容在直流电路中相当开路隔直作用,在关联参考方向下:,所以:,1.电容电压的连续性质,电容电压的连续性质,设,电容电流波形虽然不连续,但电容电压波形却是连续的。,(电容电压不能跃变),电容电压的连续性质:若电容电流 在闭区间 内为有界的,则电容电压 在开区间 内为连续的。特别是对任意时刻t,且 有:,证明,任取一点t,以t 和 t + dt 分别作为积分上下限,且 ta t tb 和 ta t + dt tb ,则,即,由于i(t)在ta, tb内为有界的,所以,对所有在 ta, tb内的t,必存在一个有限常数M,使|i(t)|M,因而,在曲线i(t)下由t 轴和上下限所界定的图形面积最大为Mdt , 且当dt0时,该面积也将趋于零。这就意味着当dt0时, ,亦即,在t处uc是连续的。,电容电压的记忆性质,i(t)是有界值,结论1:在某一时刻t 电容电压的数值并不只取决于该时刻的电流值,而是取决于从到t 所有时刻的电流值,即电容电压与电流的全部过去历史有关。电容电压具有“记忆”电流的性质,电容是一种记忆元件。,结论2:如果知道了初始时刻t0开始作用时的电流以及电容的初始电压uc(t0),就能确定 t t0 时的电容电压。,例如图(a)所示,电容与一电流源相接,电流源的波形如图(b)所示,试求电容电压。设u(0)=0。,解:,(1)先写出电流的函数表达式。,(2)根据公式 进行分段积分,解(续),解(续),电容的瞬时功率,定义:任一时刻的功率称为瞬时功率。 电容的瞬时功率为:,某一时刻电容的储能:,假设 时电容无储能,则:,结论:电容的功率有正有负,说明电容有时吸收功率,有时放出功率。,例题,电容的储能,电容储能,0 电容不断储能,0 电容向外电路释放能量,结论:电容的能量总为正,但有时增加,有时减少。电容是无源元件。,t1t2期间电容储存或释放的能量:,电容的储能,结论:t1t2期间电容储存或释放的能量只与t1、 t2时刻的电压值有关,而与此期间内的 其他电压值无关。,结论,1、电容的储能本质使电容电压具有记忆性质; 2、电容电流在有界条件下储能不能跃变,使电容电压具有连续性质。,具有初始电压的电容等效电路,结论:一个已被充电的电容,如果已知初始电压uc(t0) =U0,则在t t0时可等效为一个未充电的电容与电压源相串联的电路,电压源的电压值即为U0。又称U0为电容的初始状态。,电容的串、并联,电容的串联,根据KVL:,等效电路,其中:,为等效电路电容的初始电压,是各串联电容初始电压的代数和。,电容的串、并联,Cs 为等效电路的等效电容,其倒数为各串联电容倒数的总和。,电容的并联 (设电容初始电压为0),根据KCL可得等效电容:,为各并联电容的总和。,电容的串、并联,例题,如图所示电路中,各电容元件的电容值均为,,,试求端口ab的等效电容。,解,例题,求如图所示电路中各电容元件上的电压。已知,解 两个1F电容并联的等效电容为:,。,根据电荷平衡原理,3F上的电荷应与,相等,所以有:,上的电荷,(A),又因为,(B),(A)、(B)联立可求得:,、,5-2 电感元件,电感器(inductor),把导线绕成线圈即构成电感器(电感线圈)。,电感器是存储磁场能量的器件。,理想电感器只具有产生磁通从而建立磁场的作用,因而是一种磁链与电流相约束的器件。,电感元件,电感元件是实际电感器的理想化模型。,2.1 定义:如果在任一时刻t,一个二端元件的电流i(t)与其磁链(t)之间的关系可以用i-平面上的一条曲线确定,则称此二端元件为电感元件。,2.2 符号,考虑电阻的电感器模型:,2.3 线性非时变电感元件:电感元件的特性曲线是i-平面上的一条过原点的直线,且不随时间而变化。,电感元件,即:,2.4 电感(inductance):L,单位:亨利(H)W,A,毫亨(mH),微亨( ),或:,电感的VCR,关联参考方向:电压的参考方向与磁链的参考方向符合右手螺旋定则,电流的参考方向与磁链的参考方向符合右手螺旋定则。,结论:某一时刻,电感的电压取决于该时刻电感电流的变化率。,非关联参考方向:,电感的动态特性,电感在直流电路中相当于短路,任选初始时刻t0后,结论:某一时刻t 的电感电流值取决于其初始值i(t0)以及在区间t0, t的所有电压值。,电感的动态特性,1、在电感电压为有限值的情况下,电感电流不能跃变,将此性质称为电感电流的连续性。,电容、电感的对偶性,2、在某一时刻电感的储能为 。,假设 时电感无储能。,3、在某一时间段 电感储存或释放的能量为:,电感的串联(设电感初始电流为0),根据KVL:,电感的串、并联,等效电路,其中:,为等效电感,是各串联电感的总和。,电感的并联,根据KCL:,电感的串、并联,其中:,为等效电路电感的初始电流,是各并联电感初始电流的代数和。,Lp 为等效电路的等效电感,其倒数为各并联电感倒数的总和。,电感的串、并联,试求如图所示电路端口ab的等效电感。,例题,解,将如图(a)所示电路化为最简形式。,例题,(a),(b),解 等效电容为:,等效电感为:,等效电路如图(b)所示。,5-3 忆阻元件,至此,我们已经介绍了三种无源元件电阻R、电 容C和电感L,这些元件把电路的基本变量联系了起来 如图:,电路基本变量之间关系结构图,和q之间还没有一个元件能将其联系起来,只有,元件对偶,和q之间存在类似R、L、C的第四类基本电路元件,,并将其称为忆阻器,定义如下:,将M 称为忆阻,M是q的函数。并推出如下关系:,忆阻元件的符号下图所示。,忆阻元件,加州大学伯克利分校的华裔科学家蔡少棠,提出在,忆阻元件,忆阻器的某些基本特性为:是耗能元件;具有记忆性; 只有非线性忆阻器才有实际意义;只在交变状态才 能正常工作,直到2008年5月1日,来自惠普实验室的四位科学家在 Nature杂志上发表了题为“The missing memristor found” 的文章,宣布研制出了纳米尺度的忆阻元件。惠普实 验室发现的忆阻器可以在纳米尺度上实现开关,这将 极大地缩小存储器的体积,因此,对数字计算机的发 展可能具有深远意义。,忆阻元件,5-4 换路定则及初始值的确定,电路通常都工作在一种稳定的工作状态,如果由于 某种原因,例如电源或某部分电路的接通或断开、 电路元件参数的改变等使电路的工作状态发生变化, 使其由一种工作状态变化到另外一种工作状态,将 这种工作状态的改变称为换路 。,在换路过程中,电路中的电量随时间而变化,所以 我们把这个变化的过程称为过渡过程或瞬态。把对 电路过渡过程的分析称为电路的瞬态分析。,换路,在电容电流和电感电压为有界值的情况下,电容电压 不能跃变,电感电流不能跃变,我们将这一性质称为 换路定则。用公式表示如下:,在直流激励下,电容相当于开路,电感相当于短路, 由此可以得到,时刻的等效电路,并据此计算初始,状态,和,。,换路定则,时刻的等效电路是在 时刻将电路中的电容用电压值等于 的电压源代替,电感用电流值等于 的电流源代替,独立源则取其在 时的值得到的电路。,例题1,如图(a)所示电路,开关S在,时刻打开,S打开,前电路已处于稳态,求开关打开后电路中各元件的,电压值。,(a),解 开关打开前电容开路,所以,例题1,开关打开后的,等效电路如图(b)所示。此时,;,;,(b),例题2,求如图(a)所示电路中的,、,、,和,(a),(b),解 t = 0时,开关闭合。,时,开关未闭合,电感短路,,等效电路如图,时:,,,所示。,(b),例题2,,,,,因为,所以,的单位换算说明如下:,法拉第电磁定律:导体回路中感应电动势大小与穿过导体回路磁通量的变化率成正比,通过对前面例题的求解,可以总结出求初始值的计算步骤如下: 1)由,;,等效电路计算,和,3)画出,2)根据换路定则,,,,;,等效电路,其中,电容用电压值为,的电压源代替,电感用电流值为,的电流源,代替;,4)用分析直流电路的方法计算待求量。,计算步骤,5-5 一阶电路的零输入响应,内容提要,RC电路的零输入响应,RL电路的零输入响应,小结,几个定义,如果电路中除了电阻元件外,还含有电容、电感这些动态元件,则由于动态元件电压电流之间的微积分关系,此时就需要用微分方程进行描述。我们将至少含有一个动态元件的电路称为动态电路。通常含有一个动态元件的电路用一阶微分方程描述,称其为一阶动态电路。,1.几个定义,1.几个定义,t t0时的RC串联电路,说明:us在 t = t0时可能不连续,但电容电压却是连续的,,零输入响应,零状态响应,1.几个定义,零状态响应 (zero state response-z.s.r) :在零初始状态下,仅由外加激励引起的响应。,零输入响应(zero input response-z.i.r):在没有外加激励情况下,仅由非零初始状态引起的响应。,全响应 (complete response-c.r) :零输入响应与零状态响应之和。,因为零输入响应是依靠动态元件的初始储能进行的,所以,当电路中存在耗能元件时,有限的储能终将被消耗殆尽,零输入响应最终为零。所以,零输入响应是一个放电过程。,返回,状态变量(state variable), 电容、电感都属于动态元件元件的 VCR涉及对电压、电流的微分或积分。,至少含有一个动态元件的电路称为动态电路。, 在动态电路中,电容电压和电感电流是电 路的状态变量。, 在电路及系统理论中,状态变量是指一组最 少的变量,若已知它们在t0时刻的数值(初 始状态),则根据所有在t t0时的输入就能 确定在t t0时电路中的任何电路变量。,2.RC电路的零输入响应,KVL方程:,解得:,其中:,电路中的电流:,放电电压、电流曲线:,2.RC电路的零输入响应,2.RC电路的零输入响应,时间常数:,时间常数的单位:,称为电路的固有频率 (natural frequency),电压、电流衰减的快慢取决于时间常数的大小, 越大,衰减越慢,反之则越快。,t = 时,电压下降为初始值的36.8%。,工程上常取t = (4 5 ) 作为放电完毕所需时间。,返回,不同时间常数时的放电曲线,3.RL电路的零输入响应,KVL方程:,3.RL电路的零输入响应,放电曲线,解得:,其中:,电感电压(非关联参考方向):,电路的固有频率:,解:,根据换路定则:,返回,例题,例题,如图所示电路中,已知,;,求,时的,和,。,(a),解,时,电容开路,例题,
网站客服QQ:2055934822
金锄头文库版权所有
经营许可证:蜀ICP备13022795号 | 川公网安备 51140202000112号

