资源预览内容
space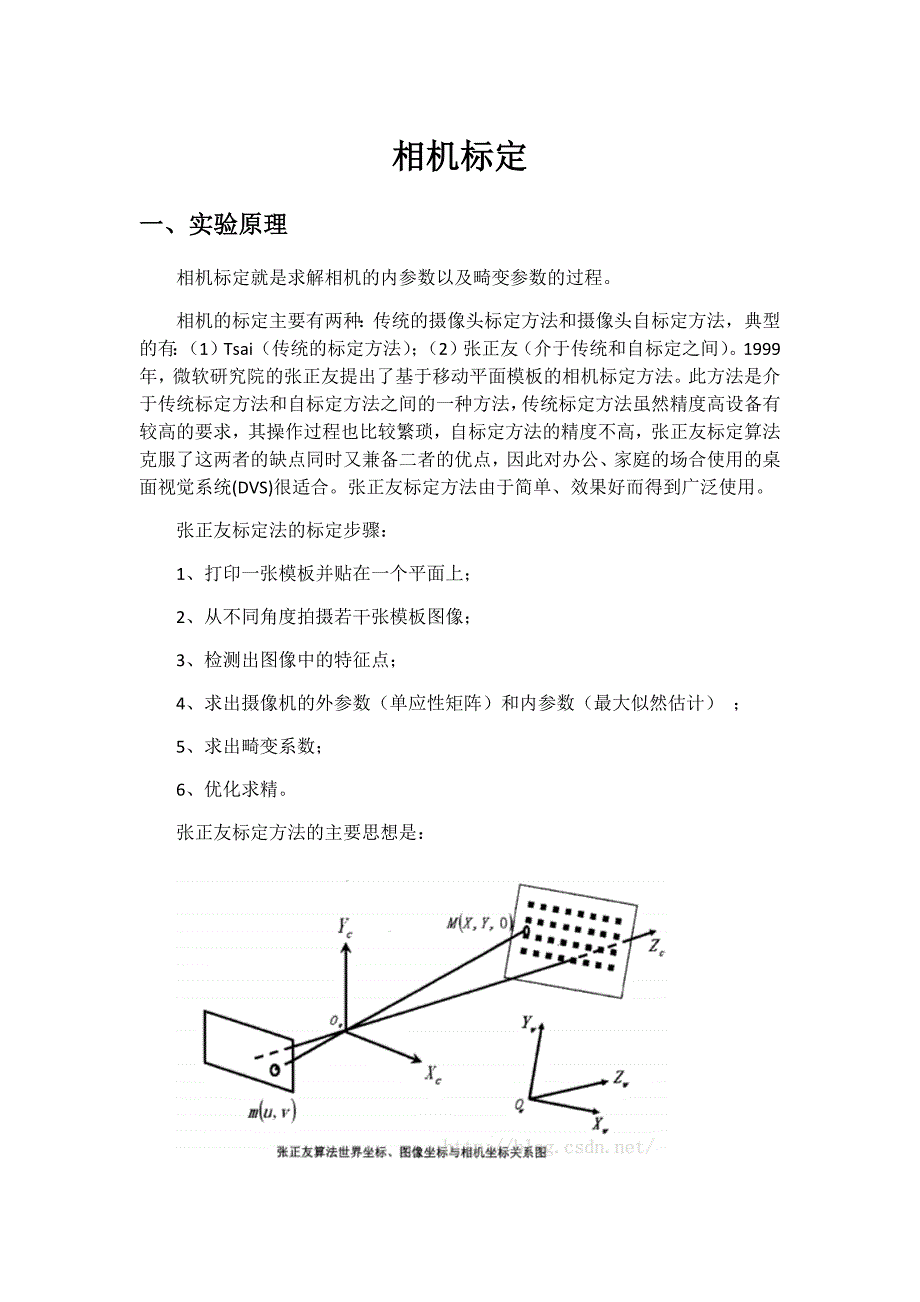
第1页 / 共14页
space
第2页 / 共14页
space
第3页 / 共14页
space
第4页 / 共14页
space
第5页 / 共14页
space
第6页 / 共14页
space
第7页 / 共14页
space
第8页 / 共14页
space
第9页 / 共14页
space
第10页 / 共14页
亲,该文档总共14页,到这儿已超出免费预览范围,如果喜欢就下载吧!
资源描述
相机标定一、 实验原理相机标定就是求解相机的内参数以及畸变参数的过程。相机的标定主要有两种:传统的摄像头标定方法和摄像头自标定方法,典型的有:(1)Tsai(传统的标定方法);(2)张正友(介于传统和自标定之间)。1999年,微软研究院的张正友提出了基于移动平面模板的相机标定方法。此方法是介于传统标定方法和自标定方法之间的一种方法,传统标定方法虽然精度高设备有较高的要求,其操作过程也比较繁琐,自标定方法的精度不高,张正友标定算法克服了这两者的缺点同时又兼备二者的优点,因此对办公、家庭的场合使用的桌面视觉系统(DVS)很适合。张正友标定方法由于简单、效果好而得到广泛使用。张正友标定法的标定步骤:1、打印一张模板并贴在一个平面上;2、从不同角度拍摄若干张模板图像;3、检测出图像中的特征点;4、求出摄像机的外参数(单应性矩阵)和内参数(最大似然估计) ;5、求出畸变系数;6、优化求精。张正友标定方法的主要思想是:1、相机内参矩阵其中,q的坐标系是默认的OpenCV的像素坐标系,Q的坐标系是标定板坐标系,Z轴为0,原点在标定板的某个内角点上(标定板上角点的坐标均为*,*,0的形式),在OpenCV 3.0中使用的是(iSqures_Size,jSquare_Size,0的形式)。其中fx和fy表示相机x轴和y轴的焦距,s表示成像平面x轴和y轴的不正交性。2、基础公式对于不同位置的棋盘格到相机的成像,可以使用下面的公式进行表示:其中,R|t表示棋盘格坐标系相对于相机坐标系的位姿。把矩阵R和写开,如下式所示:进行化简得:其中u v 1是已知量,X Y 1也是已知量,A和r1 r2 t是未知量。其中H=Ar1 r2 t又叫做单应性矩阵,可以使用下面的3中所述的方法求解。3、单应矩阵求解这里使用的方法基于最大似然准则:假设提取的m存在均值为0,噪声协方差矩阵为的高斯白噪声。则优化目标为其中其中是矩阵H的第i列,并且假设已知,求解上面的非线性优化问题可以使用LM算法。初始值求解:令,则可以重写为对于n个点,对应n个方程,Lx=0,其中x是19的,L是2n9的。x的解对应于L的最小奇异值的右奇异向量。4、求解相机内参利用约束条件求解内参矩阵A:在公式中,由于r1和r2是单位向量且是正交的,所以存在下面的关系:上面的公式写成方程组的形式如下所示:上面的等式是一个最小二乘问题,可以使用SVD求解.由于A有5个参数:,u0,v0,一个单应性矩阵对应两个约束,所以求解A需要3个单应性矩阵,也就是最小需要3幅图像(超定方程)。当然,也可以使用两个单应性矩阵,此时需要令=0。算出了b之后,可以用下面的公式求A。5、求解相机外参在上面求解了相机的内参之后,可以求出棋盘格的位姿,公式如下:在OpenCV中,上面的公式是用来求解优化参数的初始值的,最终的结果是使用优化的方法得到的。由于存在误差,还是需要迭代求解以提高精度(问题描述如下):给定棋盘格的n个图像和m个角点,并假设图像点被独立同分布的噪声影响。似然函数如下所示:其中旋转矩阵R用向量r表示(罗巨格公式)。6、相机的畸变参数求解记(u,v)为理想的像素坐标,为实际观测得到的像素坐标(受到畸变)。同样的,有归一化的相机坐标系(x,y)和。对于径向畸变:用像素坐标表示则为:写成如下形式:给定n个图像中的m个点,可以得到2mn个方程,记为Dk=d。则最小二乘方法求解:如果求解了畸变参数k1和k2,则可以求解出没有畸变的坐标,从而使用上面的方法求解位姿和内参。(畸变参数k1和k2初始化可以简单的设为0。)OpenCV的模型还包括了切向畸变,并且镜像畸变有三项。因此,OpenCV中一共有五个参数k1,k2,p1,p2,k3。7、OpenCV的标定步骤1、初始化参数求解;a、求解单应性矩阵;b、根据理论的第4步求解相机内参的初始值;c、根据理论的第5步求解相机外参的初始值;d、畸变参数设置为0。2、迭代求解总体最小二乘问题,也就是上面6所示的最小二乘问题。二、 实验结果此处只显示一张图片为例,下图为原图片、校正后的图片以及标定的图片:运行结果如下:每幅图像的标定误差:第1幅图像的平均误差:0.像素第2幅图像的平均误差:0.像素第3幅图像的平均误差:0.像素第4幅图像的平均误差:0.06671像素第5幅图像的平均误差:0.像素第6幅图像的平均误差:0.像素第7幅图像的平均误差:0.像素第8幅图像的平均误差:0.像素第9幅图像的平均误差:0.像素第10幅图像的平均误差:0.像素总体平均误差:0.像素相机内参数矩阵:4647.4, 0, 936.16; 0, 4672.9, 397.63; 0, 0, 1畸变系数:-0., -3.0159, -0., -0., -2.8699第1幅图像的旋转向量:-20.292; -4.3328; 556.22第1幅图像的旋转矩阵:-0.15893, 0.4086, -0.; -0.70445, -0.46805, -0.; -0., 0.46247, 0.87302第1幅图像的平移向量:-0.68472; -3.8378; -0.第2幅图像的旋转向量:-20.193; -4.8208; 556.71第2幅图像的旋转矩阵:-0.54095, 0.55473, -0.; -0.79489, -0.09527, -0.; -0., 0., 0.3782第2幅图像的平移向量:-0.96155; -3.1159; -0.第3幅图像的旋转向量:-20.298; -4.2478; 556.54第3幅图像的旋转矩阵:-0.12663, 0.85876, -0.; -0.26959, -0.52097, -0.41638; -0., 0., 0.86353第3幅图像的平移向量:-0.57457; -3.5706; -0.01458第4幅图像的旋转向量:-20.341; -4.4295; 556.5第4幅图像的旋转矩阵:-0.0257, 0.10076, -0.; -0.68992, -0.85406, -0.; -0., 0., 0.02044第4幅图像的平移向量:-0.77377; -3.0796; -0.第5幅图像的旋转向量:-20.561; -4.9217; 556.25第5幅图像的旋转矩阵:-0.92557, 0.75744, -0.; -0.58349, -0.75931, -0.; -0., 0., 0.26976第5幅图像的平移向量:-0.89403; -3.2065; -0.第6幅图像的旋转向量:-20.44; -4.1538; 556.01第6幅图像的旋转矩阵:-0.0148, 0.67522, -0.; -0.46359, -0.52732, -0.; -0., 0., 0.88031第6幅图像的平移向量:-0.80252; -3.3932; -0.第7幅图像的旋转向量:-20.778; -4.5682; 556.64第7幅图像的旋转矩阵:-0.78552, 0.30694, -0.; -0.93511, -0.038, -0.; -0., 0., 0.11549第7幅图像的平移向量:-0.11733; -3.7689; -0.第8幅图像的旋转向量:-20.29; -4.1399; 556.84第8幅图像的旋转矩阵:-0.51184, 0.37538, -0.; -0.71227, -0.9902, -0.; -0., 0., 0.47758第8幅图像的平移向量:-0.9184; -3.3987; -0.第9幅图像的旋转向量:-20.374; -4.2751; 556.75第9幅图像的旋转矩阵:-0.2548, 0.20396, -0.; -0.47999, -0.59641, -0.; -0., 0., 0.28623第9幅图像的平移向量:-0.08763; -3.1718; -0.第10幅图像的旋转向量:-20.698; -4.9274; 556.63第10幅图像的旋转矩阵:-0.2598, 0.07457, -0.; -0.4474, -0.28947, -0.16337; -0., 0., 0.1648第10幅图像的平移向量:-0.19461; -3.2373; -0.三、 感想通过对本次实验的完成,我对相机标定的研究有了直观的认识,这个过程充分锻炼了我分析问题的能力,对理论知识的学习能力以及编程解决实际问题的能力。我也学会了如何找出自己设计中的不足,继而去排除解决问题,这就是一个自我学习的过程。当我通过实验去学习理论知识时,自己动手得出的结论,不仅能加深我对相机标定的理解,更能加深我对此的记忆。
网站客服QQ:2055934822
金锄头文库版权所有
经营许可证:蜀ICP备13022795号 | 川公网安备 51140202000112号
