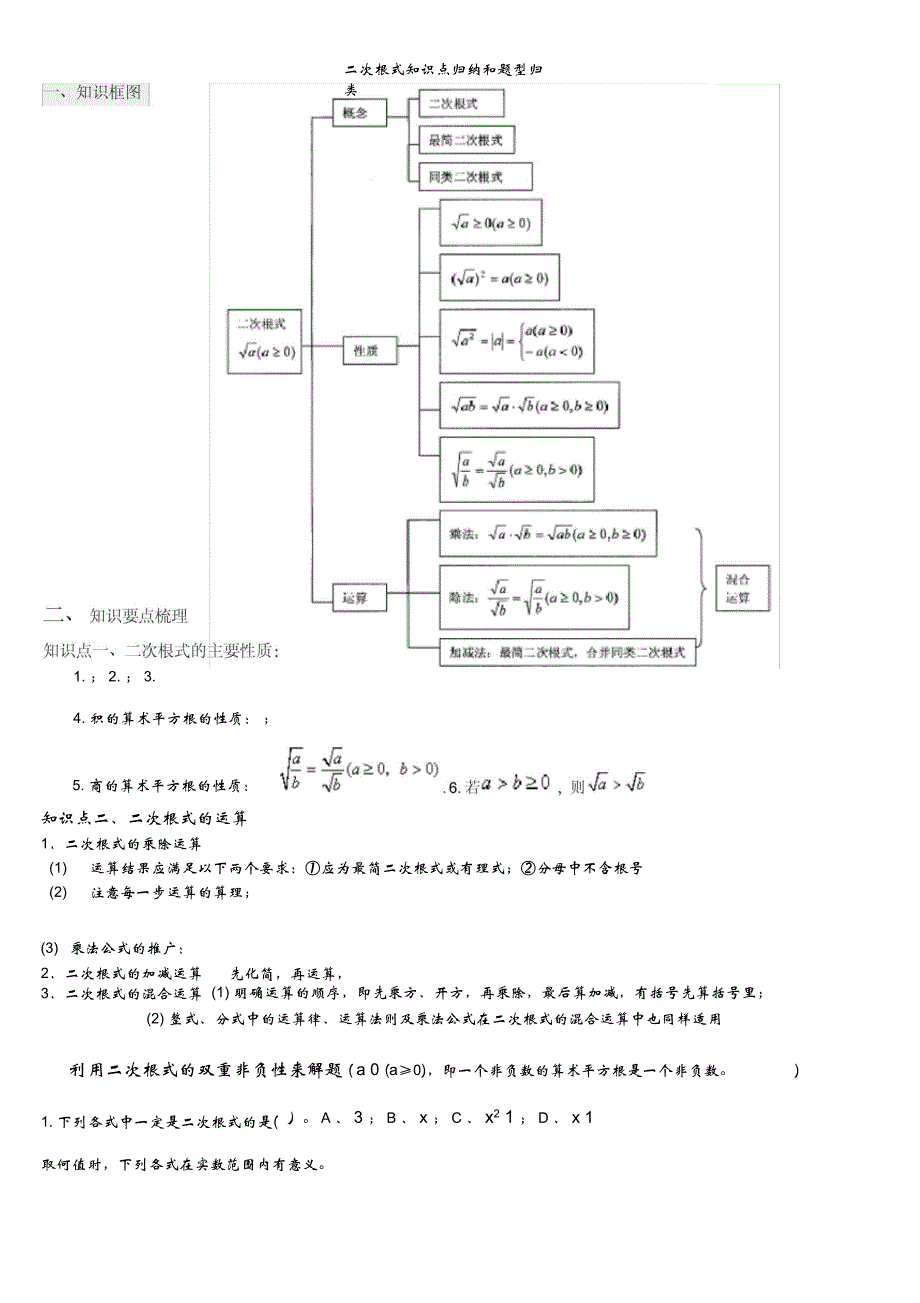
二次根式知识点归纳和题型归类1. ； 2. ； 3.4. 积的算术平方根的性质： ；5. 商的算术平方根的性质：知识点二、二次根式的运算1二次根式的乘除运算(1) 运算结果应满足以下两个要求：应为最简二次根式或有理式；分母中不含根号(2) 注意每一步运算的算理；(3) 乘法公式的推广：2二次根式的加减运算先化简，再运算，3二次根式的混合运算(1) 明确运算的顺序，即先乘方、开方，再乘除，最后算加减，有括号先算括号里；(2) 整式、分式中的运算律、运算法则及乘法公式在二次根式的混合运算中也同样适用利用二次根式的双重非负性来解题 ( a 0 (a0)，即一个非负数的算术平方根是一个非负数。)1. 下列各式中一定是二次根式的是(）。 A 、 3 ； B 、 x ； C 、 x2 1 ； D 、 x 1取何值时，下列各式在实数范围内有意义。1）（ 2）2x 11 ( 3)4)5） 3 x 1 （6） .2x 17)若 x(x 1) x x 1，则x 的取值范围是8）若 x 3 x1x 3 ，则 x 的取值范围是 x13.若 3m 1有意义，则 m能取的最小整数值是；若 20m 是个正整数， 则正整数 m的最小值是4. 当 x 为何整数时， 10x 11有最小整数值，这个最小整数值为5. 若 2004 a a 2005a ，则 a 20042 =；若 y x 3 3 x 4 ，则 x6 设 m、n 满足 n2m2 9m39 m 2 ，则 mn=7若 m 适合关系式3x 5y 2 m2x 3y m x 199 y 199 x y ，求 m 的值8. 若三角形的三边2a、b、 c 满足 a4a 4 b 3 =0，则第三边 c 的取值范围是9.已知 ABC的三边 a， b， c满足 a2| 10a 2 b 4 22 ，则 ABC 为（）10. 若 |4x 8| x y m 0，且 y 0时，则（B、m 2 C、 m二利用二次根式的性质 a2 =| a|=(a(a b)0(a 0)1. 已知 x3 3x2 x x 3 ，则() a(a 0)0即一个数的平方的算术平方根等于这个数的绝对值)来解题3. x 3D.3x02. 已知 ab，化简二次根式a3b 的正确结果是）A a ab Ba ab a ab D a ab3. 若化简 |1-x|-x2 8x 16 的结果为 2x-5 则（A、x 为任意实数 B 、1x4 Cx1 D 、x 44. 已知 a， b， c 为三角形的三边，则(a b c)2 (b c a)2 (ba）2=5. 当 -3x5 时，化简 x2 6x 9x2 10x 256、化简 |x y| x2 (x y 0) 的结果是( ) A 7、已知： a 1 2a a =1，则 a 的取值范围是(8、化简 (x 2) 1 的结果为(x 2) x 22x B y)。A、 a0；x 2 ；C、C 2xB 、 ax 2 D 、B、y1；C、a0 或 1；D 、a 1三二次根式的化简与计算 (主要依据是二次根式的性质： ( a )一)化简与求值 1. 把下列各式化成最简二次根式： ( 1)2)2x22=a( a 0)，即 a2 |a |以及混合运算法则)412 4023） 25m（4） x4 x2 y222. 下列哪些是同类二次根式： （1） 75 ，217 ， 12 ， 2， 5101102) 5 a3b3c,a3b2c3 ，acb4ca bc3. 计算下列各题：1)6 27 ( 3 3) ( 2)12ab 9a4；(3) 45ba 63cb 5ca5）12554 (6) 2ac25b2( ca3b)4.计算( 1)2 3 3 138 1 12 1 50252) (1 9x3x133y2 y3 )(4x 41x 4y4x2y53)y5已知 x 2 2 6. 1 1 1 2 2 318 x 10134二）先化简，后求值：1. 直接代入法： 已知11( 722. 变形代入法：1）变条件： 已知：，则 x 等于（ 22D 499 1005), y 1( 7 5),2求(1)x22y2(2)3 1，求 xx 1 的值。.已知 :x=322,y323222 ，求 3x2 5xy+3y2的值已知 15 x 19 x2 ，求 19 x 15 x2已知 x a 1 ，求 x 2 4x x2 a x 2 4x x22）变结论：设 3 =a， 30 =b ，则错误!= 。 y- 1 m,则1 y2的结果为（ y m, y3 ，求 x y 的值。. 已知 x 2 1, y 2 1，求x y 3 若 x y 5 3, xyy x x y 3 xy3）同时变条件与结论已知 x y 5 ， xy已知：2）求 x y 的值xy求 的值五关于求二次根式的整数部分与小数部分的问题1. 估算 312的值在哪两个数之间（）A123 C. 3 452若 3 的整数部分是 a，小数部分是 b，则 3a b3. 已知 9+ 13与9 13 的小数部分分别是 a和 b，求 ab 3a+4b+8 的值4.若a，b为有理数，且 8+ 18+ 1=a+b 2，则 ba=.817 15和 15 13六二次根式的比较大小 （1） 1 200和2 3（2） 5 6和 6 5 （5c b a D. b c a（4）设 a= 3 2, b 2 3, c 5 2, 则（ ）A. a b c B. a c b C.2 2 4 2 4 2七实数范围内因式分解： 1. 9 x25y22. 4 x44x21 3. x4+x26