资源预览内容
space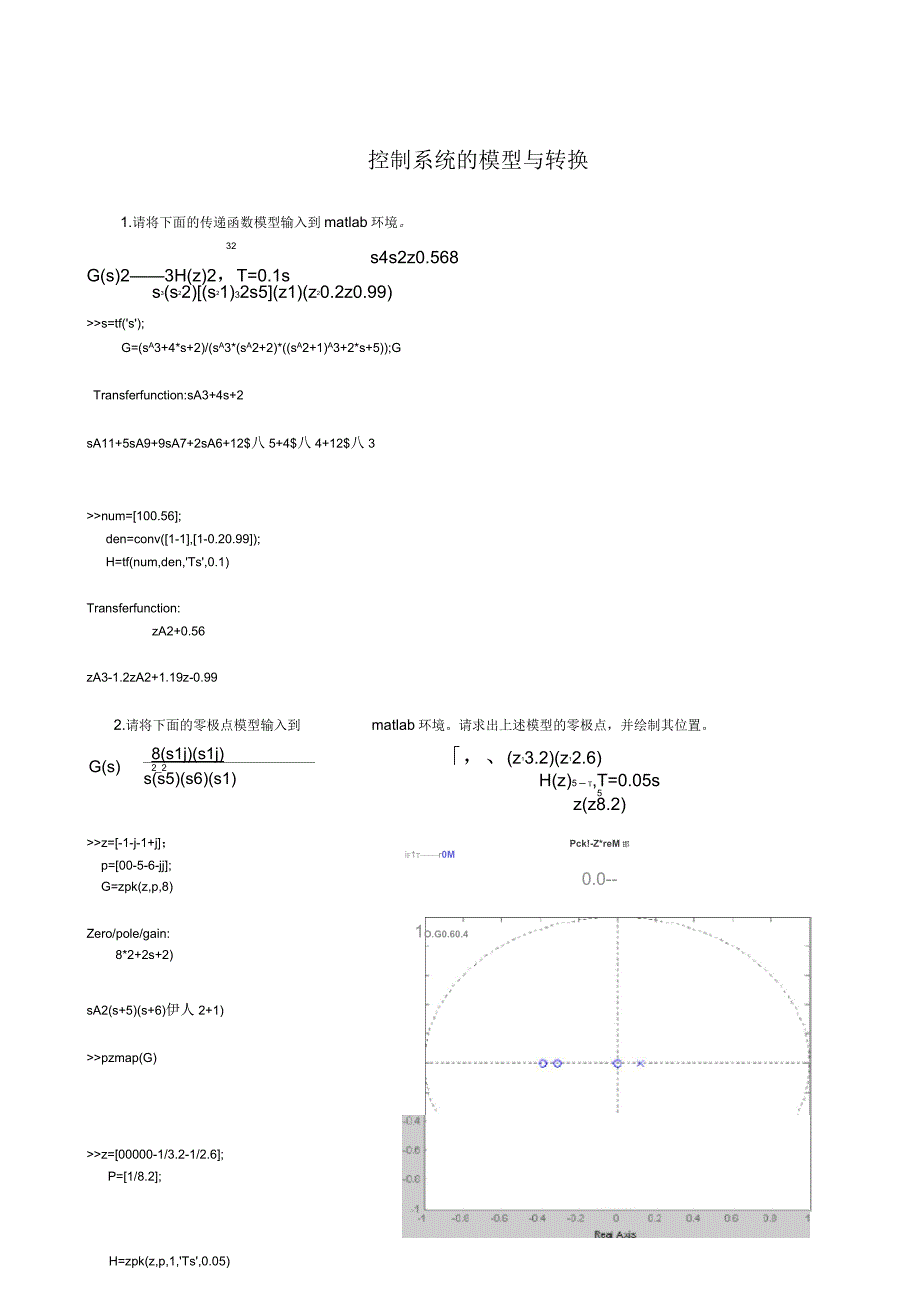
第1页 / 共28页
space
第2页 / 共28页
space
第3页 / 共28页
space
第4页 / 共28页
space
第5页 / 共28页
space
第6页 / 共28页
space
第7页 / 共28页
space
第8页 / 共28页
space
第9页 / 共28页
space
第10页 / 共28页
亲,该文档总共28页,到这儿已超出免费预览范围,如果喜欢就下载吧!
资源描述
控制系统的模型与转换1.请将下面的传递函数模型输入到matlab环境。32s4s2z0.568G(s)23H(z)2,T=0.1ss3(s22)(s21)32s5(z1)(z20.2z0.99)s=tf(s);G=(sA3+4*s+2)/(sA3*(sA2+2)*(sA2+1)A3+2*s+5);GTransferfunction:sA3+4s+2sA11+5sA9+9sA7+2sA6+12$八5+4$八4+12$八3num=100.56;den=conv(1-1,1-0.20.99);H=tf(num,den,Ts,0.1)Transferfunction:zA2+0.562.请将下面的零极点模型输入到zA3-1.2zA2+1.19z-0.99matlab环境。请求出上述模型的零极点,并绘制其位置。H=zpk(z,p,1,Ts,0.05)G(s)8(s1j)(s1j)2_2s(s5)(s6)(s1)z=-1-j-1+j;p=00-5-6-jj;G=zpk(z,p,8)Zero/pole/gain:8*2+2s+2)sA2(s+5)(s+6)伊人2+1)pzmap(G),、(z13.2)(z12.6)H(z)5一t,T=0.05s5z(z8.2)Pck!-Z*reM邯if1tr0M0.0-1O.G0.60.4z=00000-1/3.2-1/2.6;P=1/8.2;Zero/pole/gain:zA5(z+0.3125)(z+0.3846)亿-0.122)Samplingtime:0.05pzmap(H)线性系统分析1.请分析下面传递函数模型的稳定性。G(s)1332-s2ss2G(s)3s1-2Z211s(300s600s50)3s1num=1;den=1212;G=tf(num,den);eig(G)ans=-2.00000.0000-1.0000i0.0000+1.0000i可见,系统有两个特征根在虚轴上,一个特征根在虚轴左侧,所以系统是临界稳定的。num=31;den=3006005031;1PdB工5r口IVtip105Iirf-L.fKflrFde-ZEfuMBt&必0.1150.1。,&5S3-,nits由iO.HQ2r111界3JI111-1.5-1-05D0,Heelfloas5G=tf(num,den);eig(G)ans=-1.9152-0.14140.0283-0.1073i0.0283+0.1073i可见,有两个特征根在虚轴右侧,所以系统是不稳定的。2.请判定下面离散系统的稳定性。H(z)(z30.22产0.2520.05)H(z)212.12z211.76z115.91z57.368z420.15z321102.4z280.39z1340)num=-32;den=1-0.2-0.250.05;H=tf(num,den,Ts,0.1);eig(H)abs(eig(H)ans=-0.50000.50000.50000.50000.20000.2000可以看出,由于各个特征根的模均小于1,所以可以判定闭环系统是稳定的。z=tf(z,0.1);H=(2.12*zA-2+11.76*zA-1+15.91)/:(zA-5-7.368*zA-4-20.15*zA-3+102.4*zA-2+80.39*z-1-340);eig(H)abs(eig(H)ans=0000000000000000000000004.17244.17240.3755 + 0.1814i0.41700.3755 - 0.1814i0.4170-0.52920.5292-0.27160.27160.11930.1193Pule-Zelv Mb i;可以看出,由于4.1724这个特征根的模大于1,所以可以判定闭环系统是不稳定的。3.设描述系统的传递函数为G(s)18s7514s65982s536380s4122664s3222088s2185760s40320s836s7546s64536s522449s467284s3118124s2109584s40320具有零初始状态,请求出单位阶跃响应曲线和单位脉冲响应曲线。num=185145982363801226642208818576040320;den=1365464536224496728411812410958440320;G=tf(num,den)Transferfunction:18sA7+514sA6+5982sA5+36380sA4+122664sA3+22088sA2+185760s+40320sA8+36sA7+546$八6+4536$人5+22449$人4+67284$人3+118124sA2+109584s+40320step(G10)impulse(G,10)单位阶跃响应:单位脉冲响应:线性系统Simulink仿真应用1 .请分析下面传递函数模型阶跃响应。G(s)1s3 2s2 s 2利用Simulink建模,建立系统仿真模型如下:单击启动仿真按钮,双击示波器得到系统的阶跃响应如下:2 .请分析下面离散系统的脉冲响应。、3s34s21G(s)-22s2(300s2600s50)3s1利用Simulink建模,建立系统仿真模型如下:单击启动仿真按钮,双击示波器得到系统的脉冲响应如下:3 .对离散采样系统进行分析,并求出其阶跃响应其中:G(s)s 3 二2 ZZs 7 s 3s 2利用Simulink建模,建立系统仿真模型如下:Step单击启动仿真按钮,双击示波器得到系统的阶跃响应如下:4 .设计控制器,使得下列系统稳定。(s1)(s八(s3)(s2)(s1.2)利用Simulink建模,未连入控制器时,仿真模型和响应如下:25利用Simulink建模,设计控制器:Timeoffset:0从响应输出图形可以看出,连入控制器后系统稳定,性能明显提高。四、基于MATLAB的PID控制器设计设计题目:1.应用ZieglerNichols算法设计PID控制器,实现系统的闭环稳定,并比较对各个系统的控制效果。G(s)1(s 1)3未连入PID控制器时的系统仿真及其性能指标如下:StepS*1可见,未调节时的系统性能有待提高,需设计输入:num=1;den=conv(1,1,conv(1,1,1,1);Step(num,den);K=dcgain(num,den)得出:K=1根据图形,得出:L=1.86T=4.41a.3LIBM0.2D0510Tirncoffset0PID控制器连入。15如T右s4331Goooocc_oo当n言利用自定义的Ziegler_std函数求出Kp、Ti、Td输入:K=1;L=1.86;T=4.4;num,den,Kp,Ti,Td=Ziegler_std(3,K,L,T)得出:num=2.64002.83871.5262den=10Kp=2.8387Ti=3.7200Td=0.9300根据得出的Kp、Ti、Td值,设计PID控制器,并利用利用Simulink仿真建模。可见,加入PID控制器调节后,系统性能明显改善。G(s)1(s 1)5可见,未调节时的系统性能有待提高,需设计PID控制器连入。未连入PID控制器时的系统仿真及其性能指标如下:号一-0与输入:num=1;den=conv(1,1,conv(1,1,;conv(1,1,conv(1,1,1,1);Step(num,den);K=dcgain(num,den)得出:K=1根据图形,得出:L=3.4T=6.8利用自定义的Ziegler_std函数求出Kp、Ti、Td输入:K=1;L=3.4;T=6.8;num,den,Kp,Ti,Td=Ziegler_std(3,K,L,T)得出:num=4.08002.40000.7059den=1 0Kp=2.4000Ti=6.8000Td=1.7000TimeoffsM:0可见,加入PID控制器调节后,系统性能明显改善。-1.5s1G(s)3(s1)3利用Simulink建模,未连入控制器时,仿真模型和响应如下:输入:num=-1.5 1;Time (sec)den=conv(1,1,conv(1,1,1,1);Step(num,den);K=dcgain(num,den)得出:K=1根据图形,得出:L=1.8T=5.7利用自定义的Ziegler_std函数求出Kp、Ti、Td输入:K=1
网站客服QQ:2055934822
金锄头文库版权所有
经营许可证:蜀ICP备13022795号 | 川公网安备 51140202000112号
