资源预览内容
space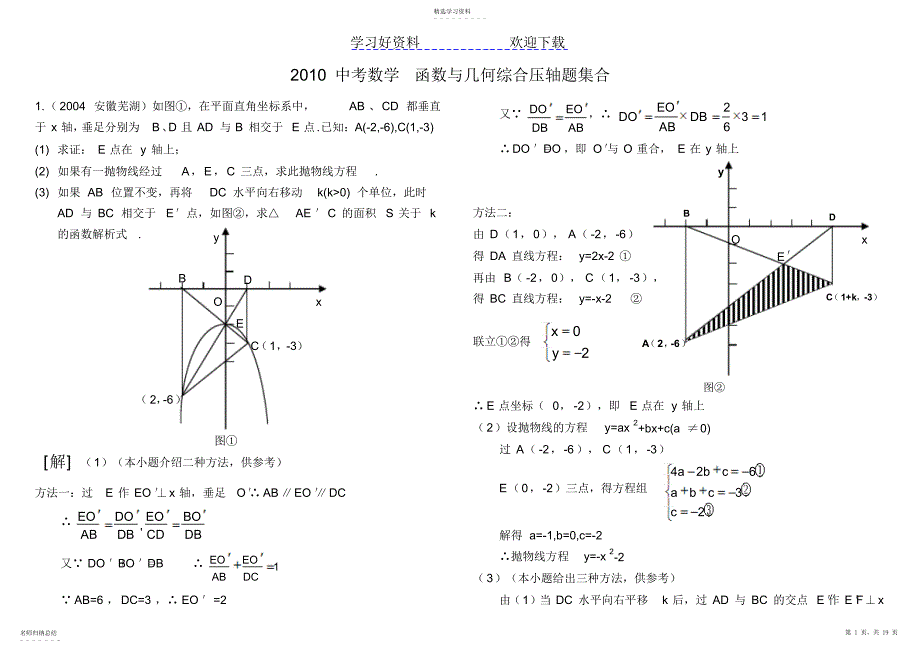
第1页 / 共19页
space
第2页 / 共19页
space
第3页 / 共19页
space
第4页 / 共19页
space
第5页 / 共19页
space
第6页 / 共19页
space
第7页 / 共19页
space
第8页 / 共19页
space
第9页 / 共19页
space
第10页 / 共19页
亲,该文档总共19页,到这儿已超出免费预览范围,如果喜欢就下载吧!
资源描述
学习好资料欢迎下载2010 中考数学函数与几何综合压轴题集合1.( 2004 安徽芜湖)如图,在平面直角坐标系中,AB 、CD 都垂直于 x 轴, 垂足分别为B、 D 且 AD 与 B 相交于 E 点.已知:A(-2,-6),C(1,-3) (1) 求证: E 点在 y 轴上;(2) 如果有一抛物线经过A,E,C 三点,求此抛物线方程. (3) 如果 AB 位置不变,再将DC 水平向右移动k(k0) 个单位,此时AD 与 BC 相交于E点,如图,求AE C 的面积S 关于 k的函数解析式. 解(1)(本小题介绍二种方法,供参考)方法一:过E 作 EO x 轴,垂足O ABEO DC ,EODOEOBOABDBCDDB又 DO + BO = DB 1EOEOABDC AB=6 , DC=3 , EO =2又DOEODBAB,2316EODODBABDO = DO ,即 O 与 O 重合, E 在 y 轴上方法二:由 D(1,0), A( -2,-6)得 DA 直线方程:y=2x-2 再由 B( -2,0), C(1, -3),得 BC 直线方程:y=-x-2 联立得02xy E 点坐标( 0, -2),即E 点在 y 轴上( 2)设抛物线的方程y=ax2+bx+c(a 0)过 A( -2,-6), C(1,-3)E(0,-2)三点,得方程组42632abcabcc解得 a=-1,b=0,c=-2 抛物线方程y=-x2-2 ( 3)(本小题给出三种方法,供参考)由(1)当 DC 水平向右平移k 后,过 AD 与 BC 的交点 E作 EFx图C (1,-3)( 2, -6)B D O x E y 图C (1+k,-3)A (2, -6)B DO x Ey 精选学习资料 - - - - - - - - - 名师归纳总结 - - - - - - -第 1 页,共 19 页学习好资料欢迎下载轴垂足为F。同( 1)可得:1E FE FABDC得: E F=2 方法一:又E FABEFDFABDB,13DFDBSAE C= S ADC- S EDC=11122223DCDBDCDFDCDB=13DCDB=DB=3+k S=3+k 为所求函数解析式方法二: BADC , S BCA=S BDA S AE C= S BDE 1132322BDE Fkk S=3+k 为所求函数解析式. 证法三: S DE CSAE C=DE AE= DC AB=1 2 同理:S DE C S DE B=12,又 S DE CS ABE=DC2AB2=1 4 2213992AE CABCDSSABCDBDk梯形 S=3+k 为所求函数解析式. 2. (2004 广东茂名)已知:如图,在直线坐标系中,以点M(1,0)为圆心、直径AC 为22的圆与y 轴交于 A、 D 两点 . (1)求点A 的坐标;(2)设过点A 的直线 yxb 与 x 轴交于点B.探究:直线AB 是否M 的切线?并对你的结论加以证明;(3) 连接 BC , 记 ABC 的外接圆面积为S1、 M 面积为 S2, 若421hSS,抛物线y ax2bx c 经过 B、 M 两点,且它的顶点到x轴的距离为h.求这条抛物线的解析式. 解( 1)解:由已知AM2, OM 1,在 Rt AOM 中, AO 122OMAM,点 A 的坐标为A(0, 1)( 2)证:直线yx b 过点 A(0,1) 10 b 即 b1y x 1 令 y0 则 x 1B( 1,0),AB2112222AOBO在 ABM 中, AB2,AM 2, BM2 222224)2()2(BMAMAB ABM 是直角三角形,BAM 90直线 AB 是 M 的切线( 3)解法一:由得BAC 90 ,AB2,AC 22,BC 10)22()2(2222ACAB BAC 90 ABC 的外接圆的直径为BC ,25)210()2(221BCS而2)222()2(222ACS421hSS,A B C D x M y 精选学习资料 - - - - - - - - - 名师归纳总结 - - - - - - -第 2 页,共 19 页学习好资料欢迎下载5,4225hh即设经过点B( 1, 0)、 M(1, 0)的抛物线的解析式为:ya( 1)( x1),( a0 )即 y ax2a, a 5, a 5 抛物线的解析式为y 5x25 或 y 5x25 解法二:(接上)求得 h5 由已知所求抛物线经过点B(1,0)、 M(1、0),则抛物线的对称轴是y 轴,由题意得抛物线的顶点坐标为(0, 5)抛物线的解析式为y a( x0)2 5 又 B( 1,0 )、 M( 1,0)在抛物线上,a 50, a 5 抛物线的解析式为y5x2 5 或 y 5x25 解法三:(接上)求得h5 因为抛物线的方程为yax2bx c(a0 )由已知得5055c0b5544002cbaaabaccbacba或解得抛物线的解析式为y5x2 5 或 y 5x25. 3.(2004湖北荆门 )如图,在直角坐标系中,以点P(1, 1)为圆心, 2为半径作圆,交x 轴于 A、B 两点,抛物线)0(2acbxaxy过点A、B,且顶点 C 在 P 上. (1)求 P 上劣弧AB的长;(2)求抛物线的解析式;(3)在抛物线上是否存在一点D,使线段OC 与 PD 互相平分?若存在,求出点D 的坐标;若不存在,请说明理由. 解( 1)如图,连结PB ,过 P 作 PM x 轴,垂足为M. 在 RtPMB 中, PB=2,PM=1, MPB 60 , APB 120AB的长342180120( 2)在 Rt PMB 中, PB=2,PM=1, 则 MB MA 3. 又 OM=1 , A(13,0), B(13,0),由抛物线及圆的对称性得知点C 在直线 PM 上,则 C(1, 3). 点 A、B、C 在抛物线上,则cbacbacba3)31()31(0)31()31(022解之得221cba抛物线解析式为222xxy( 3)假设存在点D,使 OC 与 PD 互相平分,则四边形OPCD 为平行四边形,且PC OD. A B O x y P (1, 1)A B C O x y P (1, 1)M 精选学习资料 - - - - - - - - - 名师归纳总结 - - - - - - -第 3 页,共 19 页学习好资料欢迎下载又 PC y 轴,点D 在 y 轴上, OD 2,即 D(0, 2). 又点 D(0, 2)在抛物线222xxy上,故存在点D( 0, 2),使线段OC 与 PD 互相平分 . 4.( 2004 湖北襄樊)如图,在平面直角坐标系内,Rt ABC 的直角顶点 C(0,3)在y轴的正半轴上,A、B 是x轴上是两点, 且 OA OB3 1,以 OA 、 OB 为直径的圆分别交AC 于点 E,交 BC 于点 F.直线 EF 交 OC 于点 Q. (1)求过A、B、C 三点的抛物线的解析式;(2)请猜想:直线EF 与两圆有怎样的位置关系?并证明你的猜想. (3)在 AOC 中,设点M 是 AC 边上的一个动点,过M 作 MN AB交 OC 于点N. 试问:在x轴上是否存在点P,使得 PMN是一个以MN 为一直角边的等腰直角三角形?若存在,求出 P 点坐标;若不存在,请说明理由 . 解 (1) 在 Rt ABC 中, OC AB, AOC COB. OC2OA OB. OA OB31,C(0,3), 2( 3)3.OB OBOB 1.OA 3. A(-3,0),B(1,0). 设抛物线的解析式为2.yaxbxc则930,0,3.abcabcc解之,得3,323,33.abc经过A、B、 C 三点的抛物线的解析式为:23233.33yxx(2)EF 与 O1、 O2都相切 . 证明:连结O1E、 OE、 OF. ECF AEO BFO 90 , 四边形EOFC 为矩形 . QE QO. 1 2. 3 4,2+4 90 ,EF 与 O1相切 . 同理: EF 理 O2相切 . (3)作 MP OA 于 P,设 MN a,由题意可得MP MN a. MN OA, CMN CAO. .MNCNAOCO3.33aa解之,得3 33.2a此时,四边形OPMN 是正方形 . 3 33.2MNOP3 33(,0).2P考虑到四边形PMNO 此时为正方形,点 P 在原点时仍可满足PNN 是以 MN 为一直角边的等腰直角三角形. 故x轴上存在点P 使得 PMN 是一个以MN 为一直角边的等腰直角三角形且3 33(,0)2P或(0,0).P5.(2004 湖北宜昌)如图,已知点A(0 ,1)、 C(4, 3)、E(415,823),P 是以 AC 为对角线的矩形ABCD内部 (不在各边上 )的 个动点, 点 DA y x B E F O1Q O O2C B A E F O1Q O O2y x 2 1 3 4 M P C 精选学习资料 - - - - - - - - - 名师归纳总结 - - - - - - -第 4 页,共 19 页学习好资料欢迎下载X O P D C A B Y 由方程组y=ax2 6ax+1 y=21x+1 得: ax2( 6a+21)x=0 在 y 轴,抛物线yax2+bx+1以 P 为顶点(1)说明点A、C、E 在一条条直线上;(2)能否判断抛物线yax2+bx+1的开口方向?请说明理由;(3)设抛物线y ax2+bx+1 与 x 轴有交点F、 G(F 在 G 的左侧 ), GAO与FAO的面积差为3,且这条抛物线与线段AE 有两个不同的交点这时能确定a、b 的值吗 ?若能,请求出a、b 的值;若不能,请确定 a、b 的取值范围(本题图形仅供分析参考用) 解(1)由题意, A(0 ,1)、 C(4, 3) 确定的解析式为:y=21x+1. 将点 E 的坐标E(415,823)代入y=21x+1 中,左边 =823,右边 =21415+1=823,左边 =右边,点E 在直线y=21x+1 上,即点 A、C、E 在一条直线上. (2)解法一:由于动点P 在矩形 ABCD 内部,点 P 的纵坐标大于点A 的纵坐标,而点A 与点 P 都在抛物线上,且P 为顶点,故,这条抛物线有最高点,抛物线的开口向下解法二:抛物线y=ax2+bx+c 的顶点 P 的纵坐标为aba442,且 P 在矩形 ABCD 内部, 1aba4423,由 11ab42得ab420, a 0,抛物线的开口向下. ( 3)连接 GA、FA , SGAO SFAO=3 21GO AO 21FO AO=3 OA=1 , GO FO=6. 设 F(x1,0)、 G(x2,0),则x1、x2为方程ax2+bx+c=0的两个根,且x1 x2,又 a0, x1x2=a10, x1 0 x2, GO= x2, FO= x1, x2( x1)=6 ,即 x2+x1=6, x2+x1= abab=6, b= 6a, 抛物线解析式为:y=ax2 6ax+1, 其顶点 P 的坐标为( 3,19a) , 顶点P 在矩形 ABCD 内部,11 9a3, 92 a0. x=0 或 x=aa216=6+a21. 当 x=0 时,即抛物线与线段AE 交于点 A,而这条抛物线与线段AE 有两个不同的交点,则有:0 6+a21415,解得:92 a121综合得:92 a121X G F O P D E C A B Y 精选学习资料 - - - - - - - - - 名师归纳总结 - - - - - - -第 5 页,共 19 页学习好资料欢迎下载b= 6a,21b346.(2004 湖南长沙)已知两点O(0, 0)、B(0 ,2), A 过点 B 且与 x轴分别相交于点O、 C, A 被 y 轴分成段两圆弧,其弧长之比为3 1,直线 l 与 A 切于点O,抛物线的顶点在直线l 上运动 . ( 1)求 A 的半径;( 2)若抛物线经过O、C 两点,求抛物线的解析式;( 3)过 l 上一点P 的直线与A 交于 C、E 两点,且PC CE ,求点E 的坐标;( 4)若抛物线与x 轴分别相交于C、F 两点, 其顶点P 的横坐标为m,求PEC 的面积关于m 的函数解析式. 解 (1) 由弧长之比为31,可得 BAO 90o再由 AB AO r,且 OB 2,得 r2 (2)A 的切线 l 过原点,可设l 为 ykx 任取 l 上一点 (b, kb),由 l 与 y 轴夹角为45o 可得:b kb 或 bkb ,得 k 1 或 k1,直线 l 的解析式为y x 或 yx 又由 r2,易得C(2 ,0)或 C( 2, 0) 由此可设抛物线解析式为yax(x 2)或 yax(x 2) 再把顶点坐标代入l 的解析式中得a1 抛物线为yx22x 或 yx2 2x 6 分(3)当 l 的解析式为y x 时,由 P 在 l 上,可设P(m , m)(m 0) 过 P 作 PP x 轴于 P , OP |m|,PP |m|, OP 2m2,又由切割线定理可得:OP2PC PE, 且 PC CE ,得PC PEmPP 7分C 与 P 为同一点,即PEx 轴于 C, m 2, E(2,2)8分同理,当l 的解析式为yx 时, m 2,E( 2,2) (4)若 C(2 ,0),此时l 为 y x, P 与点 O、点 C 不重合, m 0且 m 2,当 m0 时, FC 2(2m) ,高为 |yp|即为 m,S22(2)()22mmmm同理当0 m 2 时, S m22m;当 m2 时, Sm2 2m ;S222 (02)2 (02)mm mmmmm或又若 C( 2,0),此时 l 为 yx,同理可得;S222 (20)2 ( 20)mm mmmmm或7.(2006 江苏连云港) 如图, 直线4kxy与函数)0, 0(mxxmy的图像交于A、B 两点,且与x、y 轴分别交于C、 D 两点( 1)若COD的面积是AOB的面积的2倍,求k与m之间的函数关系式;( 2)在( 1)的条件下,是否存在k和m,使得以AB为直径的圆经0 x y A A 精选学习资料 - - - - - - - - - 名师归纳总结 - - - - - - -第 6 页,共 19 页学习好资料欢迎下载x y O 过点)0, 2(P若存在,求出k和m的值;若不存在,请说明理由解(1)设),(11yxA,),(22yxB(其中2121,yyxx),由AOBCODSS2,得)(2BODAODCODSSS21OC2OD(21OD1y21OD2y),)(221yyOC,又4OC,8)(221yy,即84)(21221yyyy,由xmy可得ymx,代入4kxy可得042kmyy421yy,kmyy21,8416km,即mk2又方程的判别式08416km,所求的函数关系式为mk2)0(m(2)假设存在k,m,使得以AB为直径的圆经过点)0,2(P则BPAP,过A、B分别作x轴的垂线,垂足分别为M、NMAP与BPN都与APM互余,MAPBPNRtMAPRtNPB,NBMPPNAM212122yxxy,0)2)(2(2121yyxx,0)2)(2(2121yyymym,即0)(4)(222121212yyyyyymm由( 1)知421yy,221yy,代入得01282mm,2m或6,又mk2,12km或316km,存在k,m使得以AB为直径的圆经过点)0,2(P, 且12km或316km8.(2004 江苏镇江)已知抛物线2(5)5(0)ymxmxm与 x 轴交于两点1(,0)A x、2(,0)B x12()xx,与y 轴交于点C,且AB=6. ( 1)求抛物线和直线BC 的解析式 . ( 2)在给定的直角坐标系中,画抛物线和直线BC. ( 3)若P过 A、B、C 三点,求P的半径 . MNx轴 于 点( 4 ) 抛 物 线 上 是 否 存 在 点M , 过 点M作N,使MBN被直线BC分成面积比为1 3的两部分?若存在,请求出点M 的坐标;若不存在,请说明理由. NMOPDCBA精选学习资料 - - - - - - - - - 名师归纳总结 - - - - - - -第 7 页,共 19 页学习好资料欢迎下载解(1)12122155,6.mxxxxxxmm221212520()436,36,mxxx xmm解得1251,.7mm经检验 m=1 ,抛物线的解析式为:245.yxx或:由2(5)50mxmx得,1x或5xm0,m516 ,1.mm抛物线的解析式为245.yxx由2450xx得125,1.xxA( 5,0), B( 1,0), C(0, 5). 设直线 BC 的解析式为,ykxb则5,5,0.5.bbkbk直线 BC 的解析式为55.yx(2)图象略 . (3)法一:在RtAOCD中,5,45 .OAOCOAC90BPC. 又2226,BCOBOCP的半径22613.2PB法二:由题意,圆心P 在 AB 的中垂线上,即在抛物线245yxx的对称轴直线2x上,设P( 2, h)( h0),连结 PB、PC ,则222222(12),(5)2PBhPCh,由22PBPC,即2222(12)(5)2hh,解得 h=2. ( 2, 2),PP的半径22(1 2)213PB. 法三:延长CP 交P于点 F. CF为P的直径,90 .CAFCOB又,.ABCAFCACFOCBD D,.CFACAC BCCFBCOCOC又22555 2,AC225,5126,COBC5 2262 13.5CFP的半径为13.( 4)设 MN 交直线BC 于点 E,点 M 的坐标为2( ,45),t tt则点 E的坐标为( ,55).tt若1 3,MEBENBSSDD:则1 3.ME EN:精选学习资料 - - - - - - - - - 名师归纳总结 - - - - - - -第 8 页,共 19 页学习好资料欢迎下载243 4,45(55).3ENMNttt:解得11t(不合题意舍去),25,3t5 40,.39M若3 1,MEBENBSSDD:则3 1.ME EN:21 4,454(55).EN MNttt:解得31t(不合题意舍去),415,t15,280 .M存在点 M,点 M 的坐标为5 40,39或( 15,280 ). 9. 如图, M 与 x 轴交于A、B 两点,其坐标分别为)03(,A、)01( ,B,直径 CD x 轴于 N,直线 CE 切 M 于点 C,直线 FG 切 M 于点 F,交 CE 于 G,已知点G 的横坐标为3. (1) 若抛物线mxxy22经过 A、 B、 D 三点,求m 的值及点 D 的坐标 . (2) 求直线 DF 的解析式 . (3) 是否存在过点G 的直线,使它与( 1)中抛物线的两个交点的横坐标之和等于4?若存在,请求出满足条件的直线的解析式;若不存在,请说明理由. 解 (1) 抛物线过A、B 两点,11)3(m,m=3. 抛物线为322xxy. 又抛物线过点D,由圆的对称性知点D 为抛物线的顶点. D 点坐标为)41(,. (2) 由题意知:AB=4. CD x 轴, NA=NB=2. ON=1. 由相交弦定理得:NA NB=ND NC , NC 4=2 2. NC=1. C 点坐标为)11(,. 设直线DF 交 CE 于 P,连结 CF ,则 CFP=90 . 2+3=1+4=90 . GC 、GF 是切线, GC=GF. 3= 4. 1=2. GF=GP. GC=GP. 可得 CP=8. P 点坐标为)17( ,设直线DF 的解析式为bkxy则174bkbk解得82785bk直线 DF 的解析式为:82785xyF A y x O N M G E D C P 1 2 3 4 A y x O N M G F E D C 精选学习资料 - - - - - - - - - 名师归纳总结 - - - - - - -第 9 页,共 19 页学习好资料欢迎下载(3) 假设存在过点G 的直线为11bxky,则1311bk,1311kb. 由方程组3213211xxykxky得034)2(112kxkx由题意得421k,61k. 当61k时,040,方程无实数根,方程组无实数解. 满足条件的直线不存在. 10.( 2004 山西)已知二次函数212yxbxc的图象经过点A( 3,6),并与x 轴交于点B( 1, 0)和点C,顶点为P. (1)求这个二次函数的解析式,并在下面的坐标系中画出该二次函数的图象;(2)设 D 为线段OC 上的一点,满足DPC BAC ,求点 D 坐标;(3)在 x 轴上是否存在一点M,使以M 为圆心的圆与AC 、PC 所在的直线及y 轴都相切?如果存在,请求出点M 的坐标;若不存在,请说明理由 . 解( 1)解:二次函数212yxbxc的图象过点A( 3,6),B( 1, 0),得9362102bcbc解得132bc这个二次函数的解析式为:21322yxx由解析式可求P( 1, 2), C(3,0)画出二次函数的图像( 2)解法一:易证:ACB PCD 45又已知:DPC BAC DPC BAC DCPCBCAC易求6 2,2 2,4ACPCBC43DC45333OD5,03D解法二:过A 作 AEx 轴,垂足为E. 设抛物线的对称轴交x 轴于 F. 亦可证 AEB PFD 、PEEBPFFD.易求: AE6,EB 2, PF 2 23FD25133OD5,03D( 3)存在 . 1 )过 M 作 MH AC ,MG PC 垂足分别为H、G,设 AC 交 y轴于 S, CP 的延长线交y 轴于 T SCT 是等腰直角三角形,M 是SCT 的内切圆圆心,MG MH OM 又2MCOM且 OM MC OC 23,3 23OMOMOM得3 23,0M2 )在 x 轴的负半轴上,存在一点M同理 OM OC M C,2OMOCOM得3 23OMM3 23,0即在 x 轴上存在满足条件的两个点. x O y 精选学习资料 - - - - - - - - - 名师归纳总结 - - - - - - -第 10 页,共 19 页学习好资料欢迎下载A B C M O x y 11.(2004 浙江绍兴)在平面直角坐标系中,A( 1,0),B(3,0). (1)若抛物线过A,B 两点,且与y 轴交于点(0, 3),求此抛物线的顶点坐标;(2)如图,小敏发现所有过A,B 两点的抛物线如果与y 轴负半轴交于点 C,M 为抛物线的顶点,那么ACM 与 ACB 的面积比不变,请你求出这个比值;(3)若对称轴是AB 的中垂线l 的抛物线与x 轴交于点E,F,与 y 轴交于点 C,过 C 作 CP x 轴交 l 于点 P,M 为此抛物线的顶点.若四边形 PEMF 是有一个内角为60 的菱形,求次抛物线的解析式. 解( 1)322xxy,顶点坐标为(1, 4). ( 2)由题意,设y a( x 1)( x3),即 y ax22ax 3a,A( 1,0), B( 3, 0),C(0, 3a), M(1, 4a),S ACB21 4a36a,而a 0,SACB6A 、作 MD x 轴于 D,又 S ACMSACOSOCMDSAMD 21 1 3a21(3a 4a)21 2 4aa,S ACM: S ACB1:6. ( 3)当抛物线开口向上时,设ya(x 1)2k,即 y ax22ax ak, 有菱形可知kak,ak0, k0,k2a, yax2 2ax 2a,2EF. 记 l 与 x 轴交点为D, 若 PEM 60 ,则 FEM 30 ,MD DE tan30 66,k66, a36,抛物线的解析式为666326312xxy. MT 1 1 -1 -4 -2 3 0 5 6 E -1 -2 3 C x y B D M F S G H P 精选学习资料 - - - - - - - - - 名师归纳总结 - - - - - - -第 11 页,共 19 页学习好资料欢迎下载若 PEM 120 ,则 FEM 60 ,MD DE tan60 26,k26,a6, 抛物线的解析式为266262xxy. 当抛物线开口向下时,同理可得666326312xxy,266262xxy. 12. ( 2005 北京)已知: 在平面直角坐标系xOy 中, 一次函数ykxk4的图象与x 轴交于点A,抛物线yaxbxc2经过 O、A 两点。(1)试用含a 的代数式表示b;(2)设抛物线的顶点为D,以 D 为圆心, DA 为半径的圆被x 轴分为劣弧和优弧两部分。若将劣弧沿x 轴翻折,翻折后的劣弧落在D 内,它所在的圆恰与OD 相切,求D 半径的长及抛物线的解析式;(3)设点B 是满足( 2)中条件的优弧上的一个动点,抛物线在x 轴上方的部分上是否存在这样的点P,使得POAOBA43?若存在,求出点P 的坐标;若不存在,请说明理由。解(1)解法一:一次函数ykxk4的图象与x 轴交于点A 点 A 的坐标为(4, 0)抛物线yaxbxc2经过 O、A 两点cab01640,ba4解法二:一次函数ykxk4的图象与x 轴交于点A 点 A 的坐标为( 4,0)抛物线yaxbxc2经过 O、 A 两点抛物线的对称轴为直线x2xba22ba4( 2)由抛物线的对称性可知,DO DA 点 O 在 D 上,且 DOA DAO 又由( 1)知抛物线的解析式为yaxax24点 D 的坐标为(24,a)当a0时,如图1,设 D 被 x 轴分得的劣弧为OmA,它沿 x 轴翻折后所得劣弧为OnA,显然OnA所在的圆与D 关于 x 轴对称,设它的圆心为D 点 D与点 D 也关于x 轴对称点 O 在 D上,且 D 与 D相切点 O 为切点DO OD DOA DOA 45 ADO 为等腰直角三角形OD2 2点 D 的纵坐标为2精选学习资料 - - - - - - - - - 名师归纳总结 - - - - - - -第 12 页,共 19 页学习好资料欢迎下载421242aaba,抛物线的解析式为yxx1222当a0时,同理可得:OD2 2抛物线的解析式为yxx1222综上, D 半径的长为2 2,抛物线的解析式为yxx1222或yxx1222(3)抛物线在x 轴上方的部分上存在点P,使得POAOBA43设点 P 的坐标为(x,y),且 y0 当点 P 在抛物线yxx1222上时(如图 2)点 B 是 D 的优弧上的一点OBAADO1245POAOBA4360过点 P 作 PEx 轴于点 E tantanPOEEPOEyxyx603由yxyxx31222解得:xyxy112242 364 300,(舍去)点 P 的坐标为42 364 3,当点P 在抛物线yxx1222上时(如图3)同理可得,yx3。由yxyxx31222解得:xyxy112242 364300,(舍去)点 P 的坐标为42 364 3,综上,存在满足条件的点P,点 P 的坐标为423643,或42 364 3,13. (2005 北京丰台)在直角坐标系中,O1经过坐标原点O,分别与 x 轴正半轴、y 轴正半轴交于点A、 B。( 1)如图,过点A 作O1的切线与y 轴交于点C,点 O 到直线AB精选学习资料 - - - - - - - - - 名师归纳总结 - - - - - - -第 13 页,共 19 页学习好资料欢迎下载的距离为123sin55ABC,求直线AC 的解析式;(2)若O1经过点M( 2, 2),设BOA的内切圆的直径为d,试判断d+AB的值是否会发生变化,如果不变,求出其值,如果变化,求其变化的范围。解(1)如图 1,过 O 作OGB于 G,则OG125设OAk kAOBABC309035(),sinABkOBk54,OA OBAB OGSkkkAOB23451251,OAOBAB345,A(3,0)AOB90 ,AB 是O1的直径AC切O1于 A,BA ACBAC,90在Rt ABC中cos,ABCABBCBCOCBCOB4525494C()094,设直线AC 的解析式为ykxb,则3094kbbkb3494,直线 AC 的解析式为yx3494( 2)结论:dAB的值不会发生变化设AOB的内切圆分别切OA、OB 、AB 于点 P、 Q、T,如图 2 所示y B M O1Q P O A N x T 图 2 BQBTAPATOQOPdBQBTOBdAPATOAdABBTATOBdOAdOAOBd,22222,则dABdOAOBdOAOB在 x 轴上取一点N,使 AN=OB ,连接 OM 、BM、 AM、 MN y B O1O A x C 精选学习资料 - - - - - - - - - 名师归纳总结 - - - - - - -第 14 页,共 19 页学习好资料欢迎下载MOM( , ),2 2平分AOBOM,22BOMMONAMBMMANOBM OBAN45 ,又BOMANMBOMANMANMMON,45OMNMOMN,90OAOBOAANONOMMNOM22222 24dAB的值不会发生变化,其值为4。14.( 2005福建厦门)已知:O 是坐标原点,P(m, n) (m 0)是函数 y kx(k0)上的点,过点P 作直线 PA OP 于 P,直线 PA 与 x轴的正半轴交于点A (a, 0) (am). 设 OPA 面积为 s,且 s1n44. (1)当 n 1 时,求点A 的坐标;(2)若 OP AP ,求 k 的值;(3 ) 设 n 是小于20 的整数,且kn42,求 OP2的最小值 . 解过点 P 作 PQ x 轴于 Q,则 PQ n, OQm (1) 当 n1 时,s54 a2sn52(2) 解 1: OP AP PA OP OPA 是等腰直角三角形 mna2 1n4412 an 即 n4 4n240 k2 4k40 k2 解 2: OP AP PA OP OPA 是等腰直角三角形 mn 设 OPQ 的面积为s1, 则: s1s212 mn12(1n44) 即: n4 4n240 k2 4k40 k2 (3) 解 1:PA OP , PQ OA OPQ OAP 设: OPQ 的面积为s1,则s1sPO2AO2即:12k1n44n2k2n24 (1 n44)2n2化简得: 2n42k2k n44k 0 (k2)( 2kn4) 0 k 2 或 kn42(舍去 ) 。当 n 是小于20 的整数时, k2. OP2 n2m2 n2k2n2又 m0,k 2, n 是大于 0 且小于20 的整数当 n1 时, OP25 当 n2 时, OP25 当 n3 时, OP232432949859当 n 是大于3 且小于 20 的整数时,即当n 4、5、6、 19 时,OP2精选学习资料 - - - - - - - - - 名师归纳总结 - - - - - - -第 15 页,共 19 页学习好资料欢迎下载得值分别是:42442、52452、62462、 19241921924192 1824182 32432 5 OP2的最小值是5. 解 2: OP2n2m2 n2k2n2 n222n2(n2n)2 4 当 n2n时,即当n2时, OP2最小;又 n 是整数,而当n1 时, OP2 5;n 2 时, OP25 OP2的最小值是5. 解 3:PA OP , PQ OA OPQ P AQ PQQAOQPQnammn化简得: 2n4 2k2k n44k 0 (k2)( 2kn4) 0 k2 或 kn42(舍去 ) 解 4:PA OP , PQ OA OPQ P AQ s1ss1OQ2PQ2化简得: 2n42k2 k n44k0 (k2)( 2kn4) 0 k2 或 kn42(舍去 ) 解 5:PA OP , PQ OA OPQ OAP OPOAOQOP OP2 OQ OA 化简得: 2n42k2 k n44k0 (k2)( 2kn4) 0 k 2 或 kn42(舍去 ) 15.( 2005 湖北黄冈课改)如图,在直角坐标系中,O 是原点, A、B、C 三点的坐标分别为A(18,0), B(18, 6), C( 8,6),四边形OABC是梯形,点P、Q 同时从原点出发,分别坐匀速运动,其中点P沿 OA 向终点A 运动,速度为每秒1 个单位,点Q 沿 OC、CB 向终点B 运动,当这两点有一点到达自己的终点时,另一点也停止运动。( 1)求出直线OC 的解析式及经过O、A、C 三点的抛物线的解析式。( 2)试在中的抛物线上找一点D,使得以O、 A、 D 为顶点的三角形与 AOC 全等,请直接写出点D 的坐标。( 3)设从出发起,运动了t 秒。如果点Q 的速度为每秒2 个单位,试写出点Q 的坐标,并写出此时t 的取值范围。( 4)设从出发起,运动了t 秒。当 P、Q 两点运动的路程之和恰好等于梯形OABC的周长的一半,这时,直线PQ 能否把梯形的面积也分成相等的两部分,如有可能,请求出t 的值;如不可能,请说明理由。解(1) O、C 两点的坐标分别为O0,0,C6,8设 OC 的解析式为bkxy,将两点坐标代入得:43k,0b,xy43 A,O 是x轴上两点,故可设抛物线解析式为:180 xxay再将 C6 ,8代入得:403aQP O C(8,6)B(18,6)A( 18, 0)x y 精选学习资料 - - - - - - - - - 名师归纳总结 - - - - - - -第 16 页,共 19 页学习好资料欢迎下载xxy20274032(2) D6 ,10( 3 ) 当Q在OC上 运 动 时 , 可 设Qmm43,, 依 题 意 有 :222243tmmtm58, Qtt56,58,50t当 Q 在 CB 上时,Q 点所走过的路程为t2, OC 10, CQ 102tQ 点的横坐标为228102tt, Q6,22t,105t(4)梯形 OABC 的周长为44, 当 Q 点 OC 上时,P 运动的路程为t,则Q运 动 的 路 程 为t22。 OPQ中 , OP边 上 的 高 为 :532221,5322tttOPQS梯形 OABC 的面积846101821,依题意有:2184532221tt整理得:0140222tt01404222,这样的t不存在当 Q 在 BC 上时, Q 走过的路程为t22,CQ 的长为:tt121022梯形 OCQP 的面积tt102262136 8421这样的t值不存在。综上所述,不存在这样的t值,使得P, Q 两点同时平分梯形的周长和面积16.( 2005 湖北荆门)已知:如图,抛物线mxxy332312与 x轴交于A、 B 两点,与y 轴交于C 点, ACB 90 ,( 1)求 m 的值及抛物线顶点坐标;( 2)过 A、B、C 的三点的M 交 y 轴于另一点D,连结DM 并延长交 M 于点 E,过 E 点的 M 的切线分别交x 轴、 y 轴于点F、G,求直线 FG 的解析式;( 3)在( 2)条件下,设P 为CBD上的动点( P 不与 C、D 重合),连结 PA 交 y 轴于点H,问是否存在一个常数k, 始终满足AH AP k,如果存在,请写出求解过程;如果不存在,请说明理由. 解(1)由抛物线可知,点C 的坐标为( 0,m),且 m0. 设 A(x1,0), B(x2,0).则有 x1 x23m又 OC 是 RtABC 的斜边上的高, AOC COBOBOCOCOA21xmmx,即 x1 x2 m2 m23m,解得m0或 m 3而 m0,故只能取m 3 这时,4)3(3133323122xxxy故抛物线的顶点坐标为(3, 4)A B C D E F G M x y O 精选学习资料 - - - - - - - - - 名师归纳总结 - - - - - - -第 17 页,共 19 页学习好资料欢迎下载(2)解法一:由已知可得:M(3, 0), A(3,0),B( 33,0), C(0,3), D(0, 3)抛物线的对称轴是x3,也是 M 的对称轴,连结CE DE 是 M 的直径, DCE 90 , 直线 x3, 垂直平分CE ,E 点的坐标为(23, 3)33ODOMOCOA, AOC DOM 90 , ACO MDO 30 , AC DE ACCB , CB DE 又 FG DE ,FG CB 由 B( 33,0)、 C( 0, 3)两点的坐标易求直线CB 的解析式为:yx33 3可设直线FG 的解析式为yx33 n,把( 23, 3)代入求得n 5 故直线 FG 的解析式为yx335解法二:令y0,解xx33231230 得,x13,x233即 A(3, 0), B( 33, 0)根据圆的对称性,易知:M 半径为23,M(3,0)在 Rt BOC 中, BOC 90 ,OB 33, OC 3 CBO 30 ,同理, ODM 30 。而 BME DMO , DOM 90 , DE BC DE FG,BC FG EFM CBO 30在 Rt EFM 中, MEF 90 , ME23, FEM 30 ,MF 43, OF OM MF 53,F 点的坐标为(53,0)在 Rt OFG 中, OG OF tan30 53335 G 点的坐标为(0, 5)直线FG 的解析式为yx335( 3)解法一:存在常数k 12,满足 AH AP 12。连结 CP,由垂径定理可知ACAD,精选学习资料 - - - - - - - - - 名师归纳总结 - - - - - - -第 18 页,共 19 页学习好资料欢迎下载 P ACH (或利用P ABC ACO )又 CAH PAC , ACH APC ACAPAHAC即 AC2AH AP在 RtAOC 中,AC2 AO2 OC2(3)23212 (或利用AC2AO AB3 4312AH AP 12解法二:存在常数k12 ,满足 AH AP12 设 AH x, APy 由相交弦定理得HD HC AH HP 即)()33)(33(2xyxxx化简得: xy 12 即AH AP 12A B C D E F G M x y P H O 精选学习资料 - - - - - - - - - 名师归纳总结 - - - - - - -第 19 页,共 19 页
网站客服QQ:2055934822
金锄头文库版权所有
经营许可证:蜀ICP备13022795号 | 川公网安备 51140202000112号

