资源预览内容
space
第1页 / 共20页
space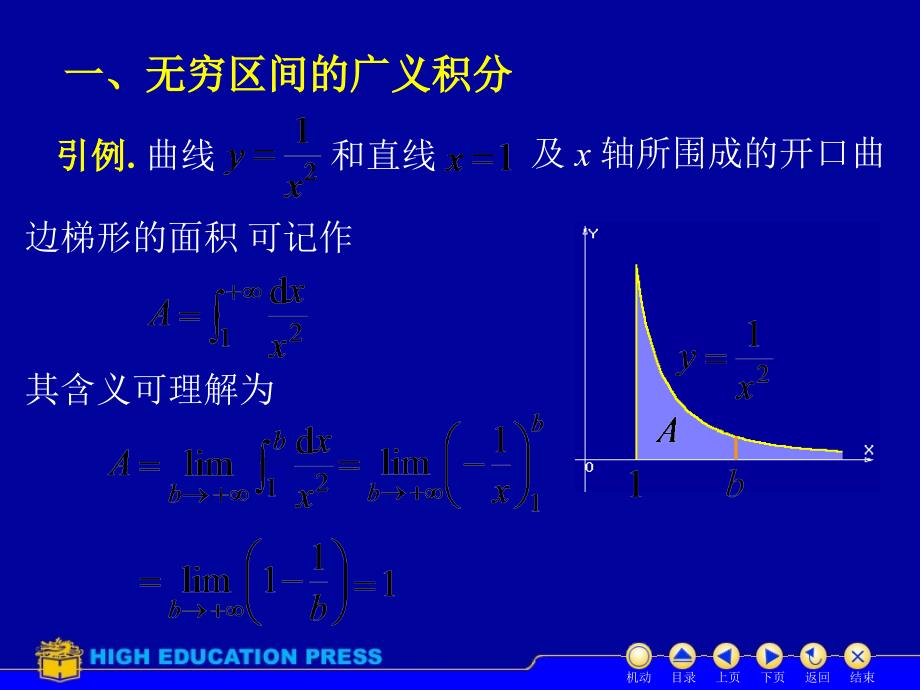
第2页 / 共20页
space
第3页 / 共20页
space
第4页 / 共20页
space
第5页 / 共20页
space
第6页 / 共20页
space
第7页 / 共20页
space
第8页 / 共20页
space
第9页 / 共20页
space
第10页 / 共20页
亲,该文档总共20页,到这儿已超出免费预览范围,如果喜欢就下载吧!
资源描述
二无界函数的广义积分教学课件Stillwatersrundeep.流静水深流静水深,人静心深人静心深Wherethereislife,thereishope。有生命必有希望。有生命必有希望一、无穷区间的广义积分一、无穷区间的广义积分引例引例. 曲线和直线及 x 轴所围成的开口曲边梯形的面积 可记作其含义可理解为 机动 目录 上页 下页 返回 结束 定义定义1. 设若存在 , 则称此极限为 f (x) 的无穷限广义积分广义积分, 记作这时称广义广义积分收敛 ;如果上述极限不存在,就称广义广义积分发散 .类似地 , 若则定义机动 目录 上页 下页 返回 结束 则定义( c 为任意取定的常数 )只要有一个极限不存在 , 就称发散 .无穷限的广义广义积分也称为第一类第一类广义广义积分积分. 并非不定型 ,说明说明: 上述定义中若出现 机动 目录 上页 下页 返回 结束 它表明该广义广义积分发散 .引入记号则有类似牛 莱公式的计算表达式 :机动 目录 上页 下页 返回 结束 例例1. 计算广义广义积分解解:机动 目录 上页 下页 返回 结束 思考思考: 分析分析:原积分发散 !注意注意: 对广义广义积分, 只有在收敛的条件下才能使用“偶倍奇零” 的性质, 否则会出现错误 .例例2. 证明第一类 p 积分证证:当 p =1 时有 当 p 1 时有 当 p 1 时收敛 ; p1 时发散 .因此, 当 p 1 时,广义广义积分收敛 , 其值为当 p1 时,广义广义积分发散 . 机动 目录 上页 下页 返回 结束 例例3. 计算广义积分解解:机动 目录 上页 下页 返回 结束 二、无界函数的二、无界函数的广义广义积分积分引例引例:曲线所围成的与 x 轴, y 轴和直线开口曲边梯形的面积可记作其含义可理解为 机动 目录 上页 下页 返回 结束 定义定义2. 设而在点 a 的右邻域内无界,存在 ,这时称广义广义积分收敛 ; 如果上述极限不存在,就称广义广义积分发散 .类似地 , 若而在 b 的左邻域内无界,若极限数 f (x) 在 a , b 上的广义广义积分, 记作则定义机动 目录 上页 下页 返回 结束 则称此极限为函 若被积函数在积分区间上仅存在有限个第一类 说明说明: 而在点 c 的无界函数的积分又称作第二类第二类广义广义积分积分, 无界点常称邻域内无界 ,为瑕点瑕点(奇点奇点) .例如,机动 目录 上页 下页 返回 结束 间断点,而不是广义广义积分. 则本质上是常义积分, 则定义注意注意: 若瑕点的计算表达式 : 则也有类似牛 莱公式的若 b 为瑕点, 则若 a 为瑕点, 则若 a , b 都为瑕点, 则则可相消吗可相消吗?机动 目录 上页 下页 返回 结束 下述解法是否正确: , 积分收敛例例4. 计算广义广义积分解解: 显然瑕点为 a , 所以原式机动 目录 上页 下页 返回 结束 例例5. 讨论广义广义积分的收敛性 . 解解:所以广义广义积分发散 .例例6. 证明广义广义积分证证: 当 q = 1 时,当 q 1 时收敛 ; q1 时发散 .当 q1 时所以当 q 1 时, 该广义积分收敛 , 其值为当 q 1 时, 该广义积分发散 .机动 目录 上页 下页 返回 结束 例例7.解解:求的无穷间断点, 故 I 为广义广义积分.机动 目录 上页 下页 返回 结束 内容小结内容小结 1.广义广义积分积分区间无限被积函数无界常义积分的极限 2. 两个重要的广义广义积分机动 目录 上页 下页 返回 结束 说明说明: (1) 有时通过换元 ,广义广义积分和常义积分可以互相转化 .例如 ,(2) 当一题同时含两类广义广义积分时,机动 目录 上页 下页 返回 结束 应划分积分区间,分别讨论每一区间上的广义广义积分. (3) 有时需考虑主值意义下的广义广义积分. 其定义为机动 目录 上页 下页 返回 结束 常积分收敛 .注意注意: 主值意义下广义广义积分存在不等于一般意义下反备用题备用题 试证, 并求其值 .解解:令机动 目录 上页 下页 返回 结束 机动 目录 上页 下页 返回 结束
网站客服QQ:2055934822
金锄头文库版权所有
经营许可证:蜀ICP备13022795号 | 川公网安备 51140202000112号

