资源预览内容
space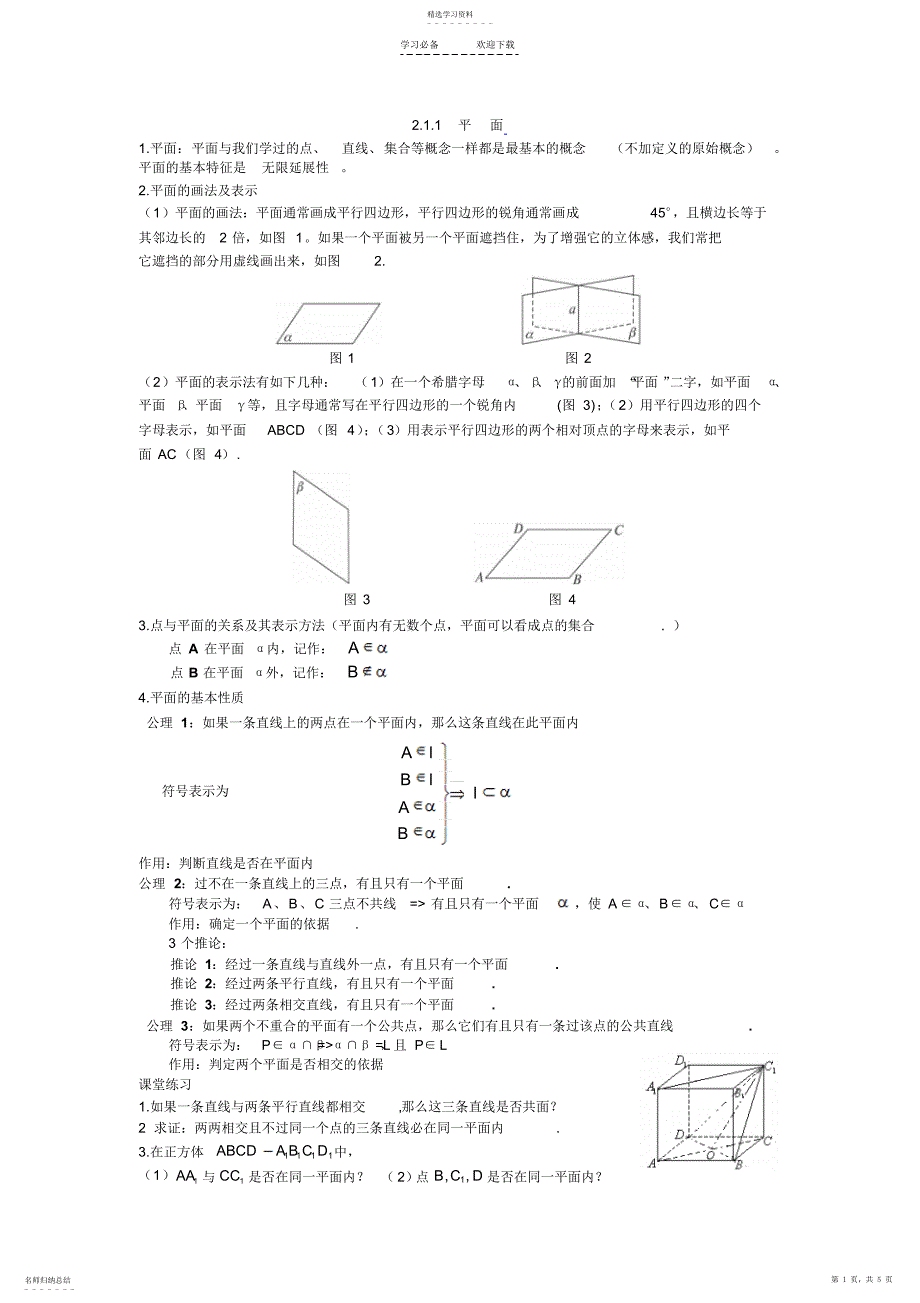
第1页 / 共5页
space
第2页 / 共5页
space
第3页 / 共5页
space
第4页 / 共5页
space
第5页 / 共5页
亲,该文档总共5页全部预览完了,如果喜欢就下载吧!
资源描述
学习必备欢迎下载2.1.1 平面1.平面:平面与我们学过的点、直线、集合等概念一样都是最基本的概念(不加定义的原始概念)。平面的基本特征是无限延展性。2.平面的画法及表示(1)平面的画法:平面通常画成平行四边形,平行四边形的锐角通常画成45 ,且横边长等于其邻边长的2 倍,如图 1。如果一个平面被另一个平面遮挡住,为了增强它的立体感,我们常把它遮挡的部分用虚线画出来,如图2. 图 1 图 2 (2)平面的表示法有如下几种:(1)在一个希腊字母 、 、 的前面加 “ 平面 ” 二字,如平面 、平面 、平面等,且字母通常写在平行四边形的一个锐角内(图 3); (2)用平行四边形的四个字母表示,如平面ABCD (图 4) ; (3)用表示平行四边形的两个相对顶点的字母来表示,如平面 AC(图 4). 图 3 图 4 3.点与平面的关系及其表示方法(平面内有无数个点,平面可以看成点的集合. )点 A 在平面 内,记作:A点 B 在平面 外,记作:B4.平面的基本性质公理 1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内符号表示为AlBllAB作用:判断直线是否在平面内公理 2:过不在一条直线上的三点,有且只有一个平面. 符号表示为:A、B、C 三点不共线 = 有且只有一个平面,使 A 、B 、 C 作用:确定一个平面的依据. 3 个推论:推论 1:经过一条直线与直线外一点,有且只有一个平面. 推论 2:经过两条平行直线,有且只有一个平面. 推论 3:经过两条相交直线,有且只有一个平面. 公理 3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线. 符号表示为:P = =L ,且 P L 作用:判定两个平面是否相交的依据课堂练习1.如果一条直线与两条平行直线都相交,那么这三条直线是否共面?2 求证:两两相交且不过同一个点的三条直线必在同一平面内. 3.在正方体1111ABCDA B C D中,(1)1AA与1CC是否在同一平面内?( 2) 点1,B CD是否在同一平面内?精选学习资料 - - - - - - - - - 名师归纳总结 - - - - - - -第 1 页,共 5 页学习必备欢迎下载(3)画出平面1AC与平面1BC D的交线,平面1ACD与平面1BDC的交线 . 解: (1)在正方体1111ABCDA B C D中,11/AACC,由公理2 的推论可知,1AA与1CC可确定平面1AC,1AA与1CC在同一平面内. (2)点1,B CD不共线,由公理3 可知,点1,B C D可确定平面1BC D, 点1,B C D在同一平面内 . (3) ACBDO,11D CDCE, 点O平面1AC,O平面1BCD,又1C平面1AC ,1C平面1BC D , 平面1AC平面1BC D1OC ,同理平面1ACD平面1BDCOE 4.已知 ABC 三边所在直线分别与平面交于 P、Q、R 三点,求证:P、Q、R 三点共线 . 解: 如图 13,A、B、C 是不在同一直线上的三点, 过 A、B、C 有一个平面.又 AB =P,且 AB,点 P 既在 内又在 内.设 =l,则 Pl, 同理可证: Ql,Rl, P、Q、R 三点共线 . 2.1.2空间中直线与直线之间的位置关系1. 空间中两条直线的位置关系共 面 直 线相交:同一平面内,有且只有一个公共点平行:同一平面内,没有公共点异 面 直 线:不同在任何一个平面内,没有公共点2. 异面直线(1)概念:不同在任何一个平面内的两条直线. (2)判断:下列各图中直线l 与 m是异面直线吗? (3)画法:用一个或两个平面衬托(4)辨析空间中没有公共点的两条直线是异面直线. 分别在两个不同平面内的两条直线是异面直线. 不同在某一平面内的两条直线是异面直线. 平面内的一条直线和平面外的一条直线是异面直线. lmlmlmlmlmlmlmlmlmlm图 13 精选学习资料 - - - - - - - - - 名师归纳总结 - - - - - - -第 2 页,共 5 页学习必备欢迎下载既不相交,又不平行的两条直线是异面直线 . 注意:判断异面直线的关键:既不相交,又不平行. 3公理 4:平行于同一条直线的两条直线互相平行。符号表示为:设a、b、c 是三条直线/abacbc注:公理4 实质上是说平行具有传递性,在平面、空间此性质都适用;公理 4 作用:判断空间两条直线平行的依据. 4. 异面直线所成的角(1)等角定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补. (2)异面直线a、b 所成的角:在空间中任取一点O ,过点O 分别引a a,b b,则 a ,b所成的 锐角(或直角)叫做两条异面直线所成的角. (3)异面直线所成的角的范围:(0,90 ,如果两条异面直线所成的角是直角,则叫两条异面直线垂直,记作ab. 注: 如果两条异面直线a , b 所成的角为直角,我们就称这两条异面直线互相垂直, 记为 a b;在求作异面直线所成的角时,O 点常选在其中的一条直线上(如线段的端点,线段的中点等)。求两条异面直线所成角的步骤可以归纳为四步:选点平移定角计算. 课堂练习1. 直线外一点可作无数条直线与已知直线成异面直线? 2. 在正方体ABCD-A1B1C1D1中, (1)哪些棱所在的直线与直线BA1成异面直线?(2)求直线BA1和 CC1所成的角的大小。 (3)哪些棱所在的直线与直线A1B垂直3. 在空间四边形ABCD中, E 、 F 分别是 AB、CD中点 , 且 EF=5 , 又 AD=6, BC=8. 求 AD与 BC所成角的余弦值.4.如图中, 正方体 ABCD A1B1C1D1,E、F 分别是 AD、AA1的中点 .(1)求直线 AB1和 CC1所成的角的大小; (2)求直线 AB1和 EF 所成的角的大小 . 解: (1)如图,连结DC1 , DC1AB1, DC1和 CC1所成的锐角CC1D 就是 AB1和 CC1所成的角 . CC1D=45, AB1和 CC1所成的角是45.(2)如图,连结DA1、A1C1, EFA1D,AB1DC1,A1DC1是直线AB1和 EF 所成的角 . A1DC1是等边三角形, A1DC1=60o,即直线AB1和 EF 所成的角是60o. 5.如图, 点 A 是 BCD 所在平面外一点,AD=BC ,E、F 分别是 AB 、CD 的中点, 且 EF=22AD ,求异面直线AD 和 BC 所成的角 .B C A D E F DCBAC A B D精选学习资料 - - - - - - - - - 名师归纳总结 - - - - - - -第 3 页,共 5 页学习必备欢迎下载6.一条直线与两条异面直线中的一条平行,则它和另一条的位置关系是()A.平行或异面B.相交或异面C.异面D. 相交7.若 a和 b 异面, b 和 c 异面,则()A.ac B.a 和 c 异面C.a 和 c 相交D.a 与 c 或平行或相交或异面7.设空间四边形ABCD , E、 F、 G、 H 分别是 AC 、 BC、 DB、 DA 的中点, 若 AB=212, CD=24,且 HG HE sinEHG=312,求 AB 和 CD 所成的角 . 解: 由三角形中位线的性质知,HG AB ,HE CD ,EHG就是异面直线AB和 CD所成的角 . 由题意可知EFGH 是平行四边形,HG=2621AB,HE=3221CD,HG HE sin EHG=612sin EHG.612sin EHG=312. sin EHG=22. 故EHG=45 .AB和 CD所成的角为45.2.1.3 、2.1.4直线与平面、平面与平面的位置关系1直线与平面有三种位置关系:(1)直线在平面内有无数个公共点(2)直线与平面相交有且只有一个公共点(3)直线在平面平行没有公共点a a=A a2两个平面之间有两种位置关系:(1)两个平面平行没有公共点(2)两个平面相交有且只有一条公共直线A B D C E F 直线在平面外a精选学习资料 - - - - - - - - - 名师归纳总结 - - - - - - -第 4 页,共 5 页学习必备欢迎下载 = L 注: 画两个相互平行的平面时,要注意使表示平面的两个平行四边形的对应边平行. 课堂练习1. 若直线 a 不平行于平面,且 a, 则下列结论成立的是( D )A. 内的所有直线与a 异面B. 内的直线与a 都相交C. 内存在唯一的直线与a 平行D. 内不存在与a 平行的直线2.若直线 a, 则下列结论中成立的个数是( A ) (1) 内的所有直线与a 异面(2) 内的直线与a 都相交(3) 内存在唯一的直线与a 平行(4) 内不存在与a 平行的直线A.0 B.1 C.2 D.3 3.若两条异面直线中的一条在平面内,讨论另一条直线与平面的位置关系 . 4. 已知 a,b,c为三条不重合的直线,为两个不重合的平面。则正确的是ab, b c a b a ,b ab a c , c a a , a5.下列命题中正确的个数是()若直线L 上有无数个点不在平面内,则 L,(2)若直线 L 与平面平行, 则 L 与平面内的任意一条直线都平行,(3)如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行,(4)若直线 L 与平面平行,则 L 与平面内任意一条直线都没有公共点(A)0 (B) 1 (C) 2 (D)3 6.已知 =l,a 且 a ,b 且 b, 又 a b=P.求证: a与 相交,b 与 相交 . 证明: 如图 14,ab=P,Pa,Pb. 又 b, P.a 与 有公共点 P,即 a与 相交 . 同理可证 ,b 与 相交 . 7.已知平面 平面 =a, b ,b a=A,c且 c a, 求证: b、c 是异面直线 . 证明: 反证法:若b 与 c 不是异面直线,则bc 或 b 与 c 相交 . (1)若 bc.ac,ab.这与 a b=A矛盾 . (2)若 b、c 相交于 B,则 B.又 a b=A, A.AB, 即 b.这与 b=A矛盾 . b,c 是异面直线 . L精选学习资料 - - - - - - - - - 名师归纳总结 - - - - - - -第 5 页,共 5 页
网站客服QQ:2055934822
金锄头文库版权所有
经营许可证:蜀ICP备13022795号 | 川公网安备 51140202000112号

