资源预览内容
space
第1页 / 共30页
space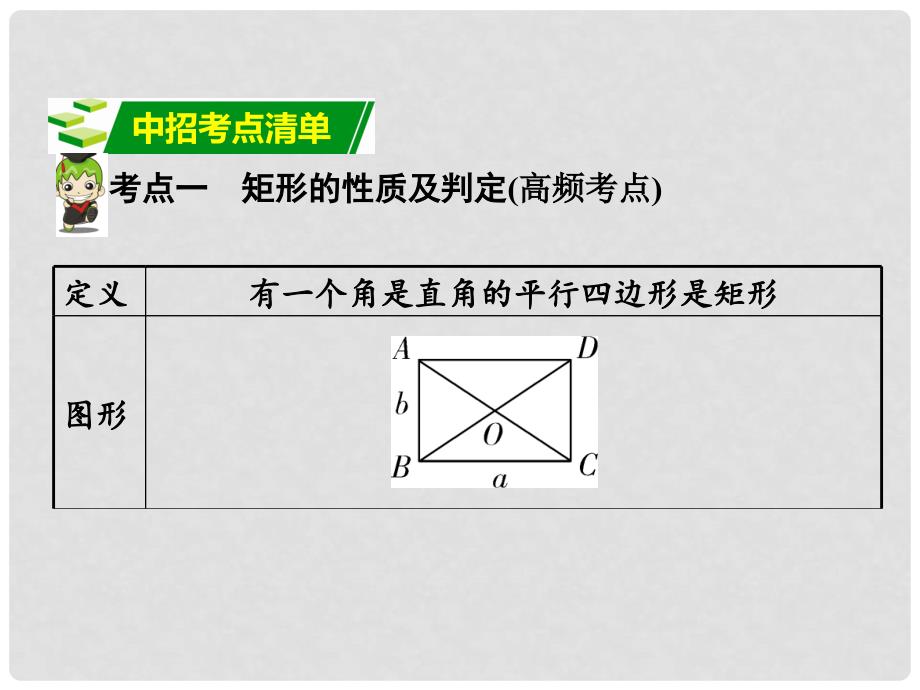
第2页 / 共30页
space
第3页 / 共30页
space
第4页 / 共30页
space
第5页 / 共30页
space
第6页 / 共30页
space
第7页 / 共30页
space
第8页 / 共30页
space
第9页 / 共30页
space
第10页 / 共30页
亲,该文档总共30页,到这儿已超出免费预览范围,如果喜欢就下载吧!
资源描述
第五章第五章 四边形四边形 第二节第二节 矩形、菱形和正方形矩形、菱形和正方形第一部分第一部分 教材知识梳理教材知识梳理中招考点清单考点一考点一 矩形的性质及判定矩形的性质及判定(高频考点高频考点)定义定义有一个角是直角的平行四边形是矩形有一个角是直角的平行四边形是矩形图形图形2性质性质1.具有平行四边形的所有性质具有平行四边形的所有性质2.边边:对边对边_且相等且相等3.角角:四个角都是四个角都是_4.对角线对角线:对角线互相平分,且对角线互相平分,且_5.既是中心对称图形,又是轴对称图形,它有既是中心对称图形,又是轴对称图形,它有_条对称轴条对称轴平行平行直角直角相等相等2判定判定1.有一个角是直角的有一个角是直角的_是矩形是矩形2.有三个角是有三个角是_的四边形是矩形的四边形是矩形3.对角线对角线_的平行四边形是矩形的平行四边形是矩形面积面积计算计算S=_(a、b分别表示矩形的长和宽分别表示矩形的长和宽)平行四边形平行四边形直角直角相等相等ab定义定义有一个角是直角的平行四边形是矩形有一个角是直角的平行四边形是矩形 考点二考点二 菱形的性质及判定菱形的性质及判定(高频考点高频考点)定义定义有一组邻边相等的平行四边形叫做菱形图形性质有一组邻边相等的平行四边形叫做菱形图形性质图形图形性质性质1.具有平行四边形的所有性质具有平行四边形的所有性质2.边边:对边平行,四边都对边平行,四边都_3.角角:对角对角_4.对角线对角线:对角线互相对角线互相 _,每条对角线,每条对角线 _一组对角一组对角5.既是中心对称图形,又是轴对称图形,它有既是中心对称图形,又是轴对称图形,它有 _条对称轴条对称轴相等相等相等相等垂直平分垂直平分2平分平分11 11 12 12 13 13 判定判定1.有一组有一组 _相等的相等的 _是菱形是菱形2. _边都相等的四边形是菱形边都相等的四边形是菱形3.对角线对角线 _的四边形是菱形的四边形是菱形面积面积计算计算S= _ (l1、l2表示对角线的长表示对角线的长)l1l2邻边邻边平行四边形平行四边形四条四条互相垂直平分互相垂直平分14 14 15 15 16 16 17 17 18 18 定义定义有一个角是直角,一组邻边相等的平行四边形叫做正有一个角是直角,一组邻边相等的平行四边形叫做正方形方形图形图形考点三考点三 正方形的性质及判定正方形的性质及判定性质性质1.既有矩形的性质,又有菱形的性质既有矩形的性质,又有菱形的性质2.边边:对边平行,四边都对边平行,四边都 _3.角角:四个角都是四个角都是 _4.对角线对角线:对角线互相对角线互相 _且相等,每条对且相等,每条对角线角线平分一组对角平分一组对角5.正方形既是轴对称图形,又是中心对称图形,正方形既是轴对称图形,又是中心对称图形,它有它有 _条对称轴条对称轴相等相等直角直角垂直平分垂直平分419 19 20 20 21 21 22 22 判定判定1.有一组有一组 _相等,并且有一个角是相等,并且有一个角是 _的平行四边形是正方形的平行四边形是正方形2.有一组邻边相等的有一组邻边相等的 _是正方形是正方形3.有一个角是直角的有一个角是直角的 _是正方形是正方形4.对角线对角线 _的平行四边形是正方的平行四边形是正方形形面积面积计算计算S= _(a表示边长表示边长)= _ (l表示对角表示对角线长线长)a2 l2邻边邻边直角直角矩形矩形菱形菱形互相垂直且相等互相垂直且相等23 23 24 24 25 25 26 26 27 27 28 28 29 29 考点四考点四 平行四边形、矩形、菱形和正方形之间的关系平行四边形、矩形、菱形和正方形之间的关系常考类型剖析类型一类型一 矩形性质的有关计算矩形性质的有关计算 (15新乡模拟新乡模拟)如图,矩形如图,矩形ABCD中,中,AB=2,BC=4,点,点E为边为边AD上一动点,把上一动点,把CDE沿沿CE折叠,当点折叠,当点D的对应点的对应点D与点与点B、E在同一条直线上时,在同一条直线上时,DE的长为的长为_.例例1例例1题图题图 【解析解析】由折叠性质可得由折叠性质可得CED=CED,DE=DE,CD=CD=2,D=CDE=90,点点D与点与点B、E在在同一直线上,同一直线上,CDB=90.在在RtBCD中,由勾股中,由勾股定理得定理得BD= 2 .又又ADBC,BCE=CED,BCE=CED,BE=BC=4,则,则DE=DE=BE-BD=4-2 .【答案答案】4-2例例1题图题图 【方法指导方法指导】对于解答矩形中的折叠问题,可以从以下对于解答矩形中的折叠问题,可以从以下3个个方面考虑:方面考虑:(1)折叠的性质:折叠的性质:位于折痕两侧的图形关于折位于折痕两侧的图形关于折痕痕(对称轴对称轴)成轴对称图形;成轴对称图形;满足折叠性质即折叠前后的满足折叠性质即折叠前后的两部分图形全等,对应边、角、线段、周长、面积都分别两部分图形全等,对应边、角、线段、周长、面积都分别相等;相等;折叠前后对应点的连线被折痕垂直平分;折叠前后对应点的连线被折痕垂直平分;(2)找出找出隐含的折叠前后的位置关系和数量关系;隐含的折叠前后的位置关系和数量关系;(3)一般运用三角一般运用三角形全等、勾股定理、相似三角形性质、特殊角的锐角三角形全等、勾股定理、相似三角形性质、特殊角的锐角三角函数等知识,以及方程思想,设比较恰当的未知数,通过函数等知识,以及方程思想,设比较恰当的未知数,通过解方程计算线段长度解方程计算线段长度.拓展题拓展题1图图 如图,矩形如图,矩形ABCD中,中,AB=8,AD=10.E是是CD上的点,将上的点,将ADE沿折痕沿折痕AE折叠,使点折叠,使点D落在落在BC边上的点边上的点F处,点处,点P是线段是线段CB延长线上的动点,连接延长线上的动点,连接PA,若,若PAF是是等腰三角形,则等腰三角形,则PB的长为的长为_.拓展题拓展题1【解析解析】四边形四边形ABCD是矩形,由折叠对称性得:是矩形,由折叠对称性得:AF=AD=10,FE=DE.在在RtABF中,中,BF= ,FC=4,要使要使PAF为等腰三角形,分三种情形讨论:为等腰三角形,分三种情形讨论:(1)若若AP=AF,ABPF,PB=BF=6;(2)若若PF=AF,则则PB+6=10,解得解得PB=4;(3)若若AP=PF,在在RtAPB中,中,AP2=PB2+AB2,即即(PB+6)2=PB2+82,解得解得PB= ,综上得综上得PB为为6或或4或或 .【答案答案】6或或4或或拓展题拓展题1图图 类型二类型二 菱形的判定菱形的判定 (15荆门荆门)已知:如图,在四边形已知:如图,在四边形ABCD中,中,ABCD,E,F为对角线为对角线AC上两点,且上两点,且AECF,DFBE,AC平分平分BAD.求证:四边形求证:四边形ABCD为菱形为菱形.例例2题图题图 例例2【思路分析思路分析】根据平行线的性质、等角的补角相等可得根据平行线的性质、等角的补角相等可得DCF=EAB,CFD=AEB,然后利用,然后利用“角边角角边角”证明证明ABE和和CDF全等,得出全等,得出AB=CD,从而得到四边,从而得到四边形形ABCD是平行四边形是平行四边形.由由AC平分平分BAD易得易得DAC=BAC=DCA根据等腰三角形等角对等边的根据等腰三角形等角对等边的性质得到性质得到DA=DC.例例2题图题图 证明证明:ABCD,BAEDCFDFBE,BECDFAAEBCFD在在AEB和和CFD中,中,BAE=DCF,AE=CF,AEB=DFC,AEBCFDABCD例例2题图题图 ABCD,四边形四边形ABCD是平行四边形是平行四边形AC平分平分BAD,BAE=DAFBAE=DCF,DAF=DCFDA=DC四边形四边形ABCD是菱形是菱形例例2题图题图 【方法指导方法指导】证明一个四边形是菱形常用的方法有:证明一个四边形是菱形常用的方法有:(1)首先判定这个四边形为平行四边形首先判定这个四边形为平行四边形(一般是全等三角形的一般是全等三角形的应用应用),再判定其邻边是否相等,或判定其对角线是否相,再判定其邻边是否相等,或判定其对角线是否相互垂直;互垂直;(2)直接证明四条边都相等直接证明四条边都相等.注意不能将两种判定注意不能将两种判定方法相混淆方法相混淆. 如图,在如图,在ABC中,中,F是是BC的中点,的中点,E是线段是线段AB的延长线上的动点,连接的延长线上的动点,连接EF,过点,过点C作作AE的平行线与线的平行线与线段段EF的延长线交于点的延长线交于点D,连接,连接CE.(1)求证:四边形求证:四边形DBEC是平行四边形;是平行四边形;(2)若已知若已知AB=BC=2,ABC=120,则在点,则在点E运动过程中:运动过程中:当当BE=_时,四边形时,四边形BDCE是矩形;是矩形;当当BE=_时,四边形时,四边形BDCE是菱形是菱形.拓展题拓展题2拓展题拓展题2图图 【思路分析思路分析】(1)首先由中点得到相等线段,再由平行线得首先由中点得到相等线段,再由平行线得到两组相等的角,利用到两组相等的角,利用“AAS”可证明可证明DCFEBF,从而从而得到对应线段相等,再结合已知条件即可得证;得到对应线段相等,再结合已知条件即可得证;(2)先由已先由已知条件可得四边形知条件可得四边形BDCE是平行四边形,再让它满足矩形是平行四边形,再让它满足矩形和菱形的特征,再根据矩形和菱形的性质可得和菱形的特征,再根据矩形和菱形的性质可得和和的解的解.(1)证明证明:F是是BC的中点的中点,BF=FC,DCAE,FDC=FEB,FCD=FBE,DCFEBF(AAS),DC=BE,四边形四边形DBEC是平行四边形;是平行四边形;拓展题拓展题2图图 (2)解解:【解法提示解法提示】由由(1)得四边形得四边形DBEC是平行四边形是平行四边形.当当CEB=90时,四边形时,四边形DBEC是矩形,是矩形, AB=BC=2,ABC=120,CBE=60,在在RtCEB中,中,BE=BCcosCBE=BCcos60=2 =1;当当CE=BE时,时,四边形四边形BDCE是菱形,是菱形,AB=BC=2ABC=120,CBE=60,CEB是等边三角形是等边三角形BE=BC=AB=2.类型三类型三 正方形性质的有关计算正方形性质的有关计算 (15长春长春)如图,点如图,点E在正方形在正方形ABCD的边的边CD上,若上,若ABE的面积为的面积为8,CE3,则线段,则线段BE的长为的长为_.例例3例例3题图题图 【解析解析】如解图,过点如解图,过点E作作EMAB于于M,四边形四边形ABCD是正方形,是正方形,AD=BC=CD=AB,EM=AD,BM=CE,ABE的面积为的面积为8, ABEM=8,解得:,解得:EM=4,即即AD=DC=BC=AB=4,CE=3,由勾股定理得:由勾股定理得:BE=例例3题解图题解图 【答案答案】5【方法指导方法指导】对于正方形性质的有关计算问题,一般注意对于正方形性质的有关计算问题,一般注意以下知识的应用:以下知识的应用:(1)四边相等,四角相等且均为四边相等,四角相等且均为90;(2)对角线垂直且相等;对角线垂直且相等;(3)对角线平分一组对角得到对角线平分一组对角得到45角;角;(4)边长与对角线的长度比为边长与对角线的长度比为1 . 如图,正方形如图,正方形ABCD的面积为的面积为4,点,点F,G分别是分别是AB,DC的中点,将点的中点,将点A折到折到FG上的点上的点P处,折痕为处,折痕为BE,点,点E在在AD上,则上,则AE长为长为_.拓展题拓展题3图图 拓展题拓展题3【解析解析】正方形正方形ABCD的面积为的面积为4,正方形正方形ABCD的边的边长为长为2,点点A折到折到FG上的点上的点P处,折痕为处,折痕为BE,BA=BP=2,ABE=PBE,点点F,G分别是分别是AB,DC的中点,的中点,FGAB,BF=1,在在RtBPF中,中,PB=2,BF=1,FPB=30,ABP=60,ABE=30,在,在RtABE中,中,AE=ABtan30=2 .拓展题拓展题3图图 【答案答案】
网站客服QQ:2055934822
金锄头文库版权所有
经营许可证:蜀ICP备13022795号 | 川公网安备 51140202000112号

