资源预览内容
space
第1页 / 共43页
space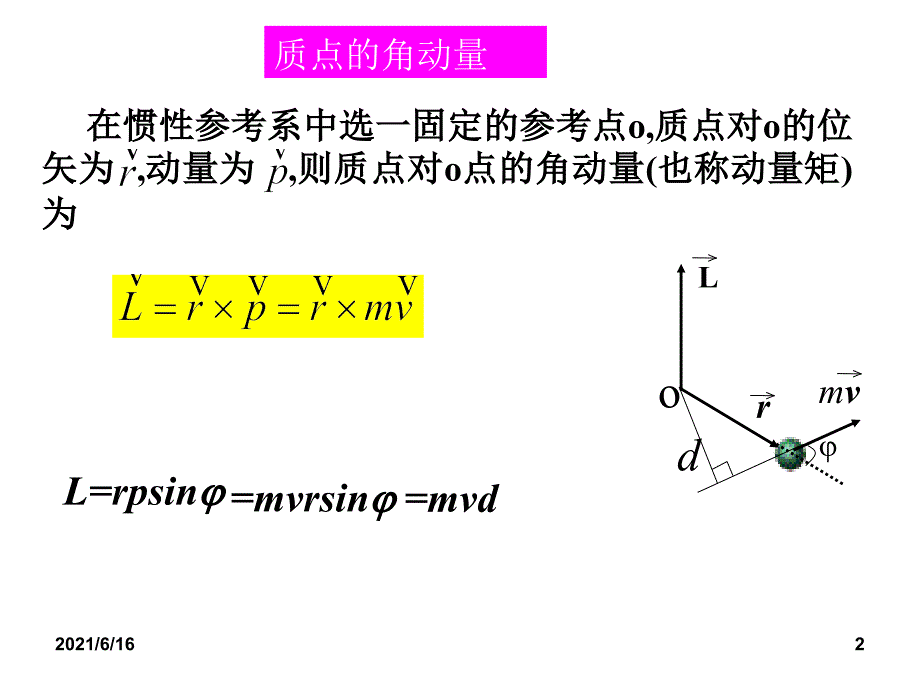
第2页 / 共43页
space
第3页 / 共43页
space
第4页 / 共43页
space
第5页 / 共43页
space
第6页 / 共43页
space
第7页 / 共43页
space
第8页 / 共43页
space
第9页 / 共43页
space
第10页 / 共43页
亲,该文档总共43页,到这儿已超出免费预览范围,如果喜欢就下载吧!
资源描述
2021/6/161Lrmvdo质点的角动量L=rpsin =mvrsin =mvd 在在惯惯性性参参考考系系中中选选一一固固定定的的参参考考点点o,质质点点对对o的的位位矢矢为为 ,动动量量为为 ,则则质质点点对对o点点的的角角动动量量(也也称称动动量量矩矩)为为2021/6/162Lrmvdo上次内容回顾2021/6/163m1mimnFnfinF1Fifnif1ifi1f1nfn1i=1,2,.n 对对n个式子求和有个式子求和有上次内容回顾2021/6/164 解解 小球对小球对o点的角动量守恒点的角动量守恒0rFom 例题例题2,如图所示,一细绳穿过光滑水平桌面上的小孔,如图所示,一细绳穿过光滑水平桌面上的小孔o,绳的一端系有一质量为,绳的一端系有一质量为m的小球并放在桌面上;另一的小球并放在桌面上;另一端用力往下拉住。设开始时小球以角速度端用力往下拉住。设开始时小球以角速度 0绕孔绕孔o作半作半径径r的匀速圆周运动的匀速圆周运动,现在向下缓慢拉绳,直到小球作圆现在向下缓慢拉绳,直到小球作圆周运动的半径为周运动的半径为r/2时止,求这一过程中拉力的功。时止,求这一过程中拉力的功。2021/6/165 解解 火箭只受引力火箭只受引力(保守力保守力)作用,机械能守恒:作用,机械能守恒: 例题例题3 质量为质量为m的火箭的火箭A,以水平速度,以水平速度 o沿地球表沿地球表面发射出去,如图所示。火箭面发射出去,如图所示。火箭A的运动轨道与地轴的运动轨道与地轴oo 相交于距相交于距o为为3R的的C点。不考虑地球的自转和空气阻力,点。不考虑地球的自转和空气阻力,求:求: =?(设地球的质量为设地球的质量为M、半径为、半径为R) Co AMRo3Rmd2021/6/166对对o点的角动量守恒:点的角动量守恒: m oR =解解得得m 3Rsin Co oAMRo3Rmd2021/6/167解:体系对解:体系对O点角动量守恒点角动量守恒已知滑轮半径为已知滑轮半径为R2021/6/168体系对体系对O点角动量守恒点角动量守恒2021/6/169 刚体的定轴转动2021/6/1610 刚刚体体的的角角动动量量=刚刚体体上上各各个个质质点点的的角角动动量量之之和和。设设刚刚体以角速度体以角速度绕固定轴绕固定轴z转动转动,质量为质量为mi的质点对的质点对o点的角动量为点的角动量为 Li=miviri=mi ri2整个刚体的角动量就是整个刚体的角动量就是 L=( mi ri2) I= mi ri2,称为称为刚体对刚体对z轴的转动惯量。轴的转动惯量。mivirioL Z刚体定轴转动的角动量2021/6/1611 I= mi ri2 即即:刚刚体体的的转转动动惯惯量量等等于于刚刚体体中中各各质质点点的的质质量量乘乘以它们各自到转轴距离的平方的总和。以它们各自到转轴距离的平方的总和。r为刚体上的质元为刚体上的质元dm到转轴的距离。到转轴的距离。质量连续分布刚体质量连续分布刚体和转轴有关和转轴有关,和物体的质量和质量分布有关和物体的质量和质量分布有关转动惯量的计算2021/6/1612lllcrommm IO=ml2+ml2=2ml2 例题例题1 质量离散分布刚体:质量离散分布刚体: I= mi ri2 (1)正三角形的各顶点处有一质点正三角形的各顶点处有一质点m,用质量不计的,用质量不计的细杆连接细杆连接,如图。系统对通过质心如图。系统对通过质心C且垂直于三角形平且垂直于三角形平面的轴的转动惯量为面的轴的转动惯量为通过通过o点且垂直于三角形平面点且垂直于三角形平面的轴的转动惯量为的轴的转动惯量为2021/6/1613Cxxdxdm 例例2质量为质量为m、长度为、长度为L的细直棒,的细直棒,求转动惯量求转动惯量(1)通通过质心过质心C且垂直于棒的轴,且垂直于棒的轴,(2)通过棒一端与棒垂直的通过棒一端与棒垂直的轴。轴。 解解 建立如图所示的坐标,将细棒分为若干微元建立如图所示的坐标,将细棒分为若干微元dm=(m/l)dx ,对棒积分得对棒积分得2021/6/1614均质圆盘均质圆盘(m,R)绕中心轴转动时,绕中心轴转动时, 均质细圆环均质细圆环(m,R)绕中心轴转动时,绕中心轴转动时,其转动惯量为其转动惯量为 质量为质量为m,长为,长为L,半径为,半径为R的均匀圆柱对通过的均匀圆柱对通过中心轴的转动惯量中心轴的转动惯量几个常见物体的转动惯量2021/6/1615 刚体对任一转轴的转动惯量刚体对任一转轴的转动惯量I等于刚体通过质心的平等于刚体通过质心的平行轴的转动惯量行轴的转动惯量Ic加上刚体的总质量加上刚体的总质量M乘以两平行轴乘以两平行轴间距离间距离d的平方,即的平方,即 I=Ic+Md2 平行轴定理2021/6/1616 平行轴定理的推导2021/6/1617 平行轴定理的推导2021/6/1618x dxCxdm 质量为质量为m、长度为、长度为L的细直棒,的细直棒,求转动惯量求转动惯量(1)通过通过质心质心C且垂直于棒的轴,且垂直于棒的轴,(2)通过棒一端与棒垂直的轴。通过棒一端与棒垂直的轴。 平行轴定理示例2021/6/1619刚体定轴转动定理对定轴转动的刚体,对定轴转动的刚体,对定轴转动来说对定轴转动来说,刚体的角加速度与它所受到的力矩正刚体的角加速度与它所受到的力矩正比比,与转动惯量成反比与转动惯量成反比这就是刚体定轴转动定理这就是刚体定轴转动定理2021/6/1620该定理在刚体力学中的地位2021/6/1621力矩问题合外力矩在合外力矩在Z轴的分量轴的分量与转轴垂直的平面与转轴垂直的平面内的力才对这个力内的力才对这个力矩有贡献矩有贡献2021/6/1622可写成积分形式2021/6/1623 刚体的进动非定轴转动问题2021/6/1624例题例题1 以以20N.m的恒力矩作用在有固定轴的转轮上,的恒力矩作用在有固定轴的转轮上,在在10s内该轮的转速均匀地由零增大到内该轮的转速均匀地由零增大到100rev/min。此时撤去该力矩,转轮经此时撤去该力矩,转轮经100s而停止。试推算此转轮而停止。试推算此转轮对该轴的转动惯量对该轴的转动惯量,及摩擦力距。及摩擦力距。 20-Mr=I 1, 1= /t1 2021/6/1625对对m: mg-T=ma对柱:对柱: TR=I , 解得解得 =2mg/(2m+M)R, T=Mmg/(2m+M)。RMmTmg 例题例题2 质量为质量为M、半径为、半径为R的匀质柱体可绕通过其中心的匀质柱体可绕通过其中心轴线的光滑水平固定轴转动;柱体边缘绕有一根不能伸长轴线的光滑水平固定轴转动;柱体边缘绕有一根不能伸长的细绳,绳子下端挂一质量为的细绳,绳子下端挂一质量为m的物体,如图所示。求柱的物体,如图所示。求柱体的角加速度及绳中的张力。体的角加速度及绳中的张力。 a=R 2021/6/1626 mg-T2= ma a=R 1=r 2 , T1R= m1R21 T2r-T1r = m2r2 2T1T1T2mgm1m2mRr12例题例题3 质量质量m1半径为半径为R的匀质圆盘可绕水平光滑轴转的匀质圆盘可绕水平光滑轴转动,一轻绳缠绕于盘上,另一端通过质量为动,一轻绳缠绕于盘上,另一端通过质量为m2半径半径r的具有水平光滑轴的圆盘形定滑轮后挂有质量为的具有水平光滑轴的圆盘形定滑轮后挂有质量为m的的物体,如图所示。求当物体物体,如图所示。求当物体m由静止开始下落了由静止开始下落了h时,时,求求:物体物体m的速度及的速度及 绳中的张力。绳中的张力。 解解 : v2=2ah,2021/6/1627 例题例题4 一根质量为一根质量为m、长为、长为l的均匀细棒的均匀细棒AB,可绕,可绕一水平光滑轴一水平光滑轴o在竖直平面内转动,在竖直平面内转动,o轴离轴离A端的距离端的距离为为 l/3。今使棒从静止开始由水平位置绕。今使棒从静止开始由水平位置绕o轴转动,求轴转动,求棒转过角棒转过角 时的角加速度和角速度。时的角加速度和角速度。 ABoCmg 解解 2021/6/1628所以完成积分得讨论讨论: (1)当当 =0时,时, =3g/2l, =0 ; (2)当当 =90时,时, =0, =(3g/l)1/2。 ABoCmg2021/6/1629 例题例题5 一质量为一质量为m、半径为、半径为R的匀质圆盘绕通过盘心的匀质圆盘绕通过盘心且垂直于盘面的光滑轴正以且垂直于盘面的光滑轴正以 o的角速度转动。现将盘的角速度转动。现将盘置于粗糙的水平桌面上,圆盘与桌面间的摩擦系数为置于粗糙的水平桌面上,圆盘与桌面间的摩擦系数为,求圆盘经转几圈将停下来?求圆盘经转几圈将停下来? rdro计算出来摩计算出来摩擦力矩是关键擦力矩是关键2021/6/1630rdro于是得于是得 又由又由 2- o2=2,所以停下来前转过的圈数,所以停下来前转过的圈数为为2021/6/1631 定轴转动的角动量守恒定律定轴转动的角动量守恒定律 若物体所受的合外力矩为零若物体所受的合外力矩为零(即即0)时,则时,则 I =常量常量 这表明:当合外力矩为零时这表明:当合外力矩为零时,物体的角动量将保持不物体的角动量将保持不变,这就是定轴转动的角动量守恒定律变,这就是定轴转动的角动量守恒定律说明:在惯性系下成立说明:在惯性系下成立2021/6/1632I I = =常量常量2021/6/1633系统定轴转动的角动量守恒系统定轴转动的角动量守恒2021/6/1634转轴存在运动的情况2021/6/1635 系统角动量守恒的条件是:系统角动量守恒的条件是: 系统动量守恒的条件是:系统动量守恒的条件是:系统的机械能守恒的条件是系统的机械能守恒的条件是:三大守恒定律的守恒条件三大守恒定律的守恒条件2021/6/1636 解解 .ommvv 例题例题5 粗糙的水平桌面上,有一长为粗糙的水平桌面上,有一长为2L、质量为、质量为m的匀质细杆,可绕通过其中点且垂直于杆的竖直的匀质细杆,可绕通过其中点且垂直于杆的竖直光滑固定轴光滑固定轴o自由转动,杆与桌面间的摩擦系数为自由转动,杆与桌面间的摩擦系数为,起初杆静止。桌面上有两个质量均为起初杆静止。桌面上有两个质量均为m的小球,的小球,各自在垂直于杆的方向上,正对着杆的一端,以相各自在垂直于杆的方向上,正对着杆的一端,以相同的速率同的速率v相向运动,并与杆的两端同时发生完全相向运动,并与杆的两端同时发生完全非弹性碰撞非弹性碰撞(设碰撞时间极短设碰撞时间极短), 如图如图,求求: (1)两小球与杆刚碰后,这一系统的角速度为多两小球与杆刚碰后,这一系统的角速度为多少?少? (2)杆经多少时间停止转动?杆经多少时间停止转动?(不计两小球重不计两小球重力造成的摩擦力矩)力造成的摩擦力矩)2021/6/1637 .ommvv (2)由= o+t:碰撞过程中有角动量守恒碰撞过程中有角动量守恒dm.ox dxfr2021/6/1638 解解 oR/2 例题例题6 匀质园盘匀质园盘(m、R)与一人与一人(m/10,视为质点视为质点)一起以角速度一起以角速度 o绕通过其盘心的竖直光滑固定绕通过其盘心的竖直光滑固定轴转动轴转动,如图所示如图所示。如果此人相对于盘以速率。如果此人相对于盘以速率v、沿半径为沿半径为R/2的园周运动的园周运动(方向与盘转动方向相反方向与盘转动方向相反), 求求:(1)圆盘对地的角速度圆盘对地的角速度;(2)欲使园盘对地静止,欲使园盘对地静止,人相对园盘的速度大小和方向?人相对园盘的速度大小和方向?2021/6/1639(2) 欲使盘静止,可令欲使盘静止,可令 oR/22021/6/1640当刚体在力矩当刚体在力矩M的作用下由角的作用下由角 1转到转到 2时时,力矩所作的功为力矩所作的功为FZdsdrop力矩的功率是力矩的功率是 P=dA/dt=Md /dt=M 定轴转动的功2021/6/1641 刚刚体体的的转转动动动动能能=刚刚体体上上各各质质点点动动能能之之和和,设设刚刚体体绕绕一一定定轴轴以以角角速速度度 转转动动,第第i个个质质点点的的质质量量为为mi,它它到到转转轴轴的的距距离离为为ri,它它的的线线速速度度vi=ri. 相应的动能相应的动能定轴转动中的动能刚体的动能是转动惯量乘以角速度刚体的动能是转动惯量乘以角速度平方的一半平方的一半2021/6/1642 结束语结束语若有不当之处,请指正,谢谢!若有不当之处,请指正,谢谢!
网站客服QQ:2055934822
金锄头文库版权所有
经营许可证:蜀ICP备13022795号 | 川公网安备 51140202000112号

