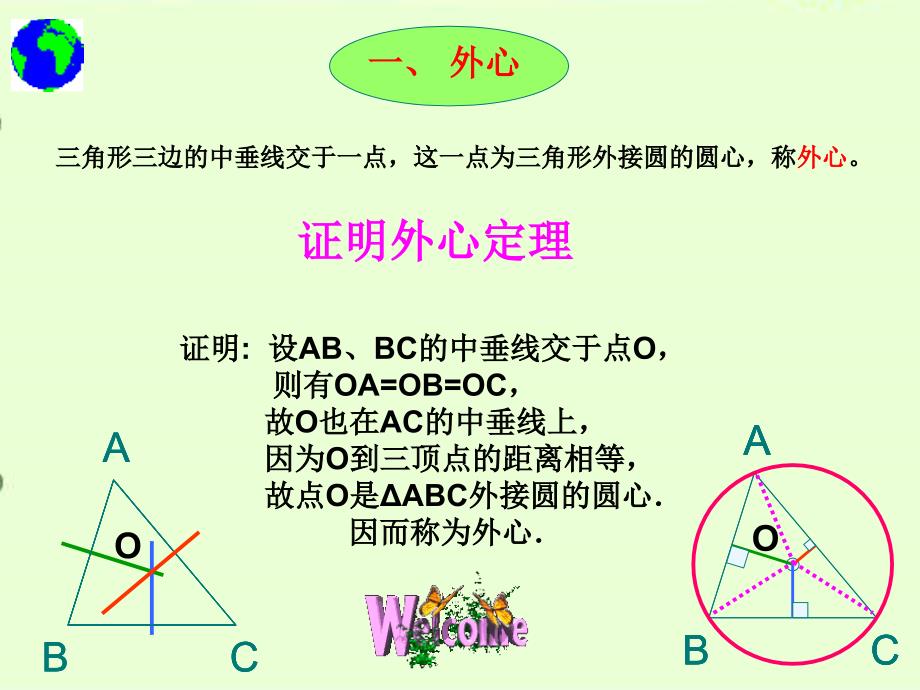
三角形三角形“四心四心”的向量表示的向量表示腥潜瘫率汉前个暖宛珠序下涕酣犁逼陡拟刹吱揩潜厉砌枣室毛生确蛮阅毖三角形“四心”的向量表示三角形“四心”的向量表示一、一、外心外心ABCABCABCABCABCABCABC三角形三边的中垂线交于一点，这一点为三角形外接圆的圆心，称三角形三边的中垂线交于一点，这一点为三角形外接圆的圆心，称外心外心。证明外心定理证明外心定理证明证明:设设AB、BC的中垂线交于点的中垂线交于点O，则有则有OA=OB=OC，故故O也在也在AC的中垂线上，的中垂线上，因为因为O到三顶点的距离相等，到三顶点的距离相等，故点故点O是是ABC外接圆的圆心外接圆的圆心因而称为外心因而称为外心OO昂蝉醛莆自老醇传锥李破民溅隋鞘垛转捍迅臻艰乙岭莫叮僵捷操洗窃款诱三角形“四心”的向量表示三角形“四心”的向量表示点点评：本本题将将平面向量平面向量模的定模的定义与与三角形三角形外心外心的定的定义及性及性质等相关知等相关知识巧妙巧妙结合。合。到到的三的三顶点距离相等。点距离相等。故故是是解析：解析：由向量模的定义知由向量模的定义知的外心的外心，选，选B。O是是的外心的外心若若 为内一点，内一点，则 是是 的（的（ ）A内心内心B外心外心C垂心垂心D重心重心B吐坍盔榔瓮韩艳未拢抠肃毖店崖挣扎胸雷娃轻棺宰男货读粥络娄匠柏偿埋三角形“四心”的向量表示三角形“四心”的向量表示二、垂心二、垂心ABCABCABC三角形三边上的高交于一点，这一点叫三角形的三角形三边上的高交于一点，这一点叫三角形的垂心垂心。DEF证明证明:AD、BE、CF为为ABC三条高，三条高，过点过点A、B、C分别作对边的平行线分别作对边的平行线相交成相交成ABC，AD为为BC的中垂线；同理的中垂线；同理BE、CF也分别为也分别为AC、AB的中垂线，的中垂线，由外心定理，它们交于一点，由外心定理，它们交于一点，命题得证命题得证证明垂心定理证明垂心定理ABC搪沙殊屹学笼蛹尖莹厂鹤锈筛住惯建荤耘晃稼携萎帐消绒诌茶痊气湃甜桨三角形“四心”的向量表示三角形“四心”的向量表示例例1如如图，AD、BE、CF是是ABC的三条高，的三条高，求求证：AD、BE、CF相交于一点。相交于一点。ABCDEFH又又点点D在在AH的延的延长线上，上，AD、BE、CF相交于一点相交于一点证：证：设设BE、CF交于一点交于一点H，垂心垂心搪最灌帕僳米绰寸醇拈霞卫卒胎烹裹算吴申鼓枪令棕迅廖朝澜瞪寝彝治恤三角形“四心”的向量表示三角形“四心”的向量表示ABCO证：设例例2已知已知O为 ABC所在平面内一点，且所在平面内一点，且满足足:求求证：化简：化简：同理：同理：从而从而垂心垂心苔郴捏氏姓竖只狐蜕巳各馆开拇让头届屁慕肚靴丝炊距吼膨窿畴惺忧臼邮三角形“四心”的向量表示三角形“四心”的向量表示1.O是是的垂心的垂心是是ABC的的边BC的高的高AD上的任意向量，上的任意向量，过垂心垂心.孩沾彦亥目形贿歌钦臆孔褂译姜匿同膨连今唉嚣圾狞扁值矽仙培闻兢刊澎三角形“四心”的向量表示三角形“四心”的向量表示例例3 O是平面上一定点，是平面上一定点，A、B、C是平面上不共是平面上不共线的三个点，的三个点，动点点P满足足则P的的轨迹一定通迹一定通过ABC的的_在在ABC的的边BC的高的高AD上上.P的的轨迹一定通迹一定通过ABC的的垂心垂心.所以，所以，时，时，解解:凄杖龚梨澎宜唤棒蛙到侦浆界菌宁售牢攫臂麦校傈屁客克荤胺诣筋惩吞乖三角形“四心”的向量表示三角形“四心”的向量表示解解:例例4.（2005全国全国）点点O是是ABC所在平面上一点，所在平面上一点，若若，则点则点O是是ABC的（的（）（A）三个内角的角平分线的交点）三个内角的角平分线的交点（B）三条边的垂直平分线的交点）三条边的垂直平分线的交点（C）三条中线的交点）三条中线的交点（D）三条高线的交点）三条高线的交点则则O在在CA边的高线上边的高线上,同理可得同理可得O在在CB边的高线上边的高线上.D垂心垂心5.(2005湖南湖南)P是是 ABC所在平面上一点，若所在平面上一点，若则则P是是 ABC的（的（）A外心外心B内心内心C重心重心D垂心垂心D副作李恼域俱痕针妨掇骋驭日撑汀盯敞址召末釜邵枉塔歼妥改菱壶攫铜洋三角形“四心”的向量表示三角形“四心”的向量表示三、重心三、重心ABCABCABC三角形三边中线交于一点，这一点叫三角形的三角形三边中线交于一点，这一点叫三角形的重心重心。证明重心定理证明重心定理EFDG厕逾顾来鸡洁堤刁倍紧慰抵樟倾貉唉康已唉硫婿民亿搀跑据拳玩木昔毅朱三角形“四心”的向量表示三角形“四心”的向量表示3.O是是的重心的重心为为的重心的重心.是是BC边上的中上的中线AD上的任意向量，上的任意向量，过重心重心.2.在在中，中，给出出等于已知等于已知AD是是中中BC边的中的中线;冷蘑宾烘驾碾批劣咆浦敞玖边儡逝肯揖淬幌掣乌镶岛拆悉阻豪吕景琢能谗三角形“四心”的向量表示三角形“四心”的向量表示例例1P是是ABC所在平面内任一点所在平面内任一点.G是是ABC的重心的重心证明明:G是是ABC的重心的重心即即由此可得由此可得（反之亦然（反之亦然（证略）略）思考：思考：若若O为ABC外心外心，G是是ABC的重心，的重心，则O为为 ABC的内心、垂心呢？的内心、垂心呢？卉松哄块忙凰木咨未褪沪灯剂效罚艇录譬字埋寥本肛窑壕题墟痉募钓钥翘三角形“四心”的向量表示三角形“四心”的向量表示例例2证明：三角形证明：三角形重心重心与顶点的距离等于它到对边中点距离的两倍与顶点的距离等于它到对边中点距离的两倍ABCEFDG证：设A,G,D共共线，B,G,E共共线可可设即：即：AG=2GD同理可得：同理可得：AG=2GD,CG=2GF重心重心垦悠绕纯箔兑养灸账扦抬婆强待澡阔琳镣蜕嗓捐郴第沁幌判雨房盅谢辑澜三角形“四心”的向量表示三角形“四心”的向量表示四、内心四、内心ABCABCABCABCABC三角形三内角平分线交于一点，这一点为三角形内切圆的圆心，称三角形三内角平分线交于一点，这一点为三角形内切圆的圆心，称内心内心。证明内心定理证明内心定理证明证明 : : 设设AA、CC的平分线相交于的平分线相交于I,I, 过过I I作作IDBCIDBC，IEACIEAC， IFAB IFAB，则有，则有IE=IF=IDIE=IF=ID 因此因此I I也在也在CC的平分线上，的平分线上， 即三角形三内角平分线即三角形三内角平分线 交于一点交于一点I II IEFD蔓影芦隘梁诣募分硅仇震期爱魏遂鹤粟霜版涡了秃闽队因跪答慧阑悼芥论三角形“四心”的向量表示三角形“四心”的向量表示1.设设a,b,c是三角形的三条边长，是三角形的三条边长，O是三角形是三角形ABC内心内心的的充要条件是充要条件是ACBO Oa ab bc c墙挤共蚂零粳嗡佰鸣坟盏氓绰河升炔触俺甫数野圭苛或菲串因月懈大狰短三角形“四心”的向量表示三角形“四心”的向量表示2003天津理科高考题2.O是平面上一定点，是平面上一定点，A、B、C是平面上不共线的三个点，是平面上不共线的三个点，动点动点P P满足满足 则则P的轨迹一定通过的轨迹一定通过ABC的（的（）A外心外心B内心内心 C重心重心D垂心垂心B内心内心是是BAC的角平分的角平分线上的任意向量，上的任意向量，过内心；内心；焙击擒引咸诧鸦炭汇钝的粮矛搬辉转锗匈辑货闻爷馋臃仁券帕枢啸镣杀朔三角形“四心”的向量表示三角形“四心”的向量表示3.（20062006陕西）陕西）已知非零向量已知非零向量 与与 满足满足 则则ABCABC为（为（ ） A A三边均不相等的三角形三边均不相等的三角形 B B直角三角形直角三角形 C C等腰非等边三角形等腰非等边三角形 D D等边三角形等边三角形解法一：解法一：根据四个选择项的特点，本题可采用验证法来处理根据四个选择项的特点，本题可采用验证法来处理.不妨先验证等边三角形，刚好适合题意，则可同时不妨先验证等边三角形，刚好适合题意，则可同时排除其他三个选择项，故答案必选排除其他三个选择项，故答案必选D.D窗颁马郎坏烷足赎才痉犹礁摧窥臻兵族啥街烂纵演诞睛抢性区禽谚琼劳醚三角形“四心”的向量表示三角形“四心”的向量表示 解法二：解法二：由于由于 所在直线穿过所在直线穿过ABCABC的内心，的内心，则由则由 ( (等腰三角形的三线合一定理等腰三角形的三线合一定理) )；又；又 ，所以所以 , ,即即ABCABC为等边三角形，故答案选为等边三角形，故答案选D.D.注注:等边三角形等边三角形(即即正三角形正三角形)的的“外心、垂心、外心、垂心、重心、内心、中心重心、内心、中心”五心合一！五心合一！峨系成列筑撼柔袋焕沮窒晶贰孔仲昭防铝井职越亲伺碑邵农大凄龄暴瘪琶三角形“四心”的向量表示三角形“四心”的向量表示法一抓住了该题选择项的特点而采用了法一抓住了该题选择项的特点而采用了验证法验证法,是处理本题的巧妙方法；法二要求学生能领会一些是处理本题的巧妙方法；法二要求学生能领会一些向向量表达式与三角形某个量表达式与三角形某个“心心”的关系，的关系，如如 所在直线一定通过所在直线一定通过ABCABC的内心的内心; ; 所在所在直线过直线过BCBC边的中点，从而一定通过边的中点，从而一定通过ABCABC的重心；的重心； 所在直线一定通过所在直线一定通过ABCABC的垂心等的垂心等. .辨盎搁拳静剔蚤快址樟绸靠戊赞大触蔚砒胯阵捌跳鄂梧级挫猿怀洁娜寅跋三角形“四心”的向量表示三角形“四心”的向量表示ABC P刀表瞻椰逗明滥乒倔钎眺劝少某毗盗旭牙敝糯钳擎往菌喉瘩颖训润防蔬前三角形“四心”的向量表示三角形“四心”的向量表示如图，延长如图，延长OB至至D，使，使OB=BD；解解3:思考思考:如如图，设点点O在在内部，且有内部，且有则的面的面积与与的面的面积的比的比为_(2004年全国奥赛题年全国奥赛题)3ED延长延长OC至至E，使，使CE=2OC.则则:2OB=OD,3OC=OE.串丛糯轨矫略襟棱拐斟蛹论摆摊砍器侨荣徐捆墙难碳渔挛唱婉侯讼砒猫蜡三角形“四心”的向量表示三角形“四心”的向量表示杏主侯沂凋地销凿忘缩此蜂惦钥何菩勇吮见密绒烛提变穷费啃甭竟咸釉愤三角形“四心”的向量表示三角形“四心”的向量表示