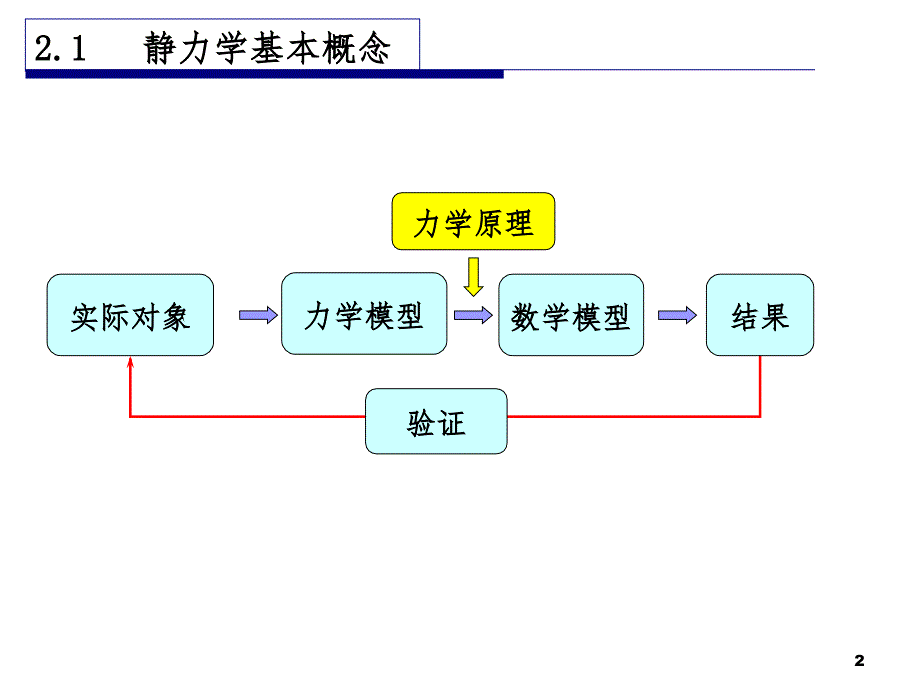
第第2章章 力的性质及物体的受力分析力的性质及物体的受力分析n2.1 静力学基本概念静力学基本概念n2.2 力的性质力的性质n2.3 物体的受力分析和受力图物体的受力分析和受力图n2.4 共点力的合成共点力的合成n2.5 力对点的矩和力对轴之矩力对点的矩和力对轴之矩n2.6 力偶力偶1实际对象实际对象验证验证力学原理力学原理结果结果数学模型数学模型力学模型力学模型2.1 2.1 静力学基本概念静力学基本概念22.1 2.1 静力学基本概念静力学基本概念静力学静力学(statics)(statics)是研究物体在力系作用下的平衡规律。是研究物体在力系作用下的平衡规律。主要任务主要任务物体的受力分析物体的受力分析力系的等效与简化力系的等效与简化力系的平衡条件力系的平衡条件32.1 2.1 静力学基本概念静力学基本概念一、一、力力(force)的概念的概念1定义：力是物体间的相互机械作用。定义：力是物体间的相互机械作用。2. 力的效应：力的效应： 运动效应运动效应( (外效应外效应) ) 变形效应变形效应( (内效应内效应) )3. 力的三要素：大小，方向，作用点力的三要素：大小，方向，作用点42.1 2.1 静力学基本概念静力学基本概念A力的单位力的单位：牛顿：牛顿(N)、千牛顿、千牛顿(kN)表示沿力矢量方向的单位向量表示沿力矢量方向的单位向量 52.1 2.1 静力学基本概念静力学基本概念等效力系等效力系 作用在物体上的一个力系与另一个力系对作用在物体上的一个力系与另一个力系对物体的作用效果相同，则称这两个力系为等效力系。物体的作用效果相同，则称这两个力系为等效力系。合力合力 (resultant force) 某力系与一个力等效，则此力某力系与一个力等效，则此力称为该力系的合力称为该力系的合力。力系力系 (force system ) 是指作用在物体上的一群力。是指作用在物体上的一群力。62.1 静力学基本概念静力学基本概念就是在力的作用下，大小和形状都不变的物体。就是在力的作用下，大小和形状都不变的物体。二二. .刚体刚体(rigid body) 是指物体相对于惯性参考系保持静止或作匀速直线是指物体相对于惯性参考系保持静止或作匀速直线运动的状态。运动的状态。 三三. .平衡平衡 (balance)平衡力系平衡力系 使物体处于平衡状态的力系使物体处于平衡状态的力系.72.2 2.2 静力学公理静力学公理AAA最简单力系的合成法则最简单力系的合成法则公理一公理一 力的平行四边形法则力的平行四边形法则 作用在物体上同一点的两个力，可以合成为一个作用在物体上同一点的两个力，可以合成为一个合力。合力的作用点也在该点，合力的大小和方向，合力。合力的作用点也在该点，合力的大小和方向，由这两个力为边构成的平行四边形的对角线确定。由这两个力为边构成的平行四边形的对角线确定。力的三角形法则力的三角形法则 8公理二公理二 二力平衡条件二力平衡条件2.2 2.2 静力学公理静力学公理最简单力系的平衡条件最简单力系的平衡条件 作用在刚体上的两个力使刚体保持平衡的必要和充分作用在刚体上的两个力使刚体保持平衡的必要和充分条件是：这两个力的大小相等，方向相反，且作用在条件是：这两个力的大小相等，方向相反，且作用在同一直线上。同一直线上。二力杆说明说明：对刚体来说，上面的条件是充要的对刚体来说，上面的条件是充要的 二力构件：只在两个力作用下二力构件：只在两个力作用下平衡的构件叫二力构件或二力杆。平衡的构件叫二力构件或二力杆。对变形体来说，上面的条件只是必要条件对变形体来说，上面的条件只是必要条件二力构件二力构件9AB2.2 2.2 静力学公理静力学公理公理三公理三 加减平衡力系公理加减平衡力系公理推论推论1 力的可传性力的可传性对刚体而言对刚体而言,力是力是滑移矢量滑移矢量，力的三要素为大小、方向和作用线，力的三要素为大小、方向和作用线 在已知力系上加上或减去任意的平衡力系，并不改变对在已知力系上加上或减去任意的平衡力系，并不改变对刚体的作用。刚体的作用。 作用于刚体上某点的力，可以沿着它的作用线移到作用于刚体上某点的力，可以沿着它的作用线移到刚体内任意一点，并不改变该力对刚体的作用。刚体内任意一点，并不改变该力对刚体的作用。BABA102.2 2.2 静力学公理静力学公理推论推论2 2 三力平衡汇交定理三力平衡汇交定理 作用于刚体上三个相互平衡的力，若其中两作用于刚体上三个相互平衡的力，若其中两个力的作用线汇交于一点，则此三力必在同一平个力的作用线汇交于一点，则此三力必在同一平面内，且第三个力的作用线通过汇交点。面内，且第三个力的作用线通过汇交点。112.2 2.2 静力学公理静力学公理公理四公理四 作用力和反作用力定律作用力和反作用力定律 两物体间相互作用的力，即作用力和反作用两物体间相互作用的力，即作用力和反作用力总是同时存在，且大小相等、方向相反，沿同力总是同时存在，且大小相等、方向相反，沿同一直线分别作用在两个物体上。一直线分别作用在两个物体上。公理五公理五 刚化原理刚化原理 变形体变形体在某一力系作用下处于平衡，如将此在某一力系作用下处于平衡，如将此变形体刚化为刚体，其平衡状态保持不变。变形体刚化为刚体，其平衡状态保持不变。处于平衡状态的变形体，可用刚体静力学的平衡理论处于平衡状态的变形体，可用刚体静力学的平衡理论进行分析进行分析122.3 2.3 物体的受力分析和受力图物体的受力分析和受力图一、约束和约束反力一、约束和约束反力约束约束(constraint)对非自由体的某些位移起限制性条件的对非自由体的某些位移起限制性条件的周围物体。周围物体。 约束反力约束反力 ( (constraint force)constraint force)当物体有运动趋势时，约当物体有运动趋势时，约束与该物体产生相互作用。束与该物体产生相互作用。自由体：自由体：位移不受限制的物体。位移不受限制的物体。非自由体：非自由体：位移受给定条件限制的物体。位移受给定条件限制的物体。主动力主动力促使物体产生运动促使物体产生运动/ /运动趋势的力，也称载荷运动趋势的力，也称载荷( (如承受的负载、自重如承受的负载、自重) )。132.3 2.3 物体的受力分析和受力图物体的受力分析和受力图大小常常是未知的；大小常常是未知的；方向总是与约束限制的物体的位移方向相反；方向总是与约束限制的物体的位移方向相反；作用点在物体与约束相接触的那一点。作用点在物体与约束相接触的那一点。约束反力特点：约束反力特点：GGN1N2142.3 2.3 物体的受力分析和受力图物体的受力分析和受力图二、常见约束类型及约束反力二、常见约束类型及约束反力1 1）柔索约束）柔索约束柔绳、链条、胶带构成的约束柔绳、链条、胶带构成的约束 柔性体约束只能承受拉力柔性体约束只能承受拉力，所以它们的约束反力是作用在接所以它们的约束反力是作用在接触点触点，方向沿柔性体轴线方向沿柔性体轴线，背离背离被约束物体被约束物体。是离点而去的力是离点而去的力。152.3 2.3 物体的受力分析和受力图物体的受力分析和受力图162 2）理想光滑面约束）理想光滑面约束2.3 2.3 物体的受力分析和受力图物体的受力分析和受力图172.3 2.3 物体的受力分析和受力图物体的受力分析和受力图约束反力作用在接触点处，方向沿公法线，指向约束反力作用在接触点处，方向沿公法线，指向受力物体是向点而来的力。受力物体是向点而来的力。NP182.3 2.3 物体的受力分析和受力图物体的受力分析和受力图齿齿 轮轮 啮啮 合合 力力滑槽与销钉滑槽与销钉N N193 3）光滑圆柱铰链约束）光滑圆柱铰链约束2.3 2.3 物体的受力分析和受力图物体的受力分析和受力图其约束特性为轴与孔的配合问题，称作光滑圆柱铰链约其约束特性为轴与孔的配合问题，称作光滑圆柱铰链约束束202.3 2.3 物体的受力分析和受力图物体的受力分析和受力图固定铰支座固定铰支座约束特点：实质是两光滑圆弧表面约束。销与孔约束特点：实质是两光滑圆弧表面约束。销与孔在某点接触，有光滑面约束反力特点，约束反力在某点接触，有光滑面约束反力特点，约束反力作用在接触点上，作用线在接触点的公法线上，作用在接触点上，作用线在接触点的公法线上，指向物体。指向物体。21 当外界载荷不同时，接触点会变，则约束力的大小与方向均有改变可用二个通过轴心的正交分力可用二个通过轴心的正交分力 表示表示222.3 2.3 物体的受力分析和受力图物体的受力分析和受力图23辊轴支座辊轴支座2.3 2.3 物体的受力分析和受力图物体的受力分析和受力图242.3 2.3 物体的受力分析和受力图物体的受力分析和受力图含销钉含销钉孔孔约束特点：由两个各穿孔的构件及圆柱销钉组成约束特点：由两个各穿孔的构件及圆柱销钉组成活动铰链活动铰链252.3 2.3 物体的受力分析和受力图物体的受力分析和受力图4 4）轴承约束轴承约束向心轴承向心轴承262.3 2.3 物体的受力分析和受力图物体的受力分析和受力图272.3 2.3 物体的受力分析和受力图物体的受力分析和受力图止推轴承止推轴承282.3 2.3 物体的受力分析和受力图物体的受力分析和受力图5 5）球铰链）球铰链A AB BN NY YX XZ Z292.3 2.3 物体的受力分析和受力图物体的受力分析和受力图三、物体的受力分析和受力图三、物体的受力分析和受力图1 1、物体的受力分析、物体的受力分析、物体的受力分析、物体的受力分析 在工程实际中，为了求出未知的约束反力，需在工程实际中，为了求出未知的约束反力，需在工程实际中，为了求出未知的约束反力，需在工程实际中，为了求出未知的约束反力，需要根据已知力，应用平衡条件求解，为此，首先要根据已知力，应用平衡条件求解，为此，首先要根据已知力，应用平衡条件求解，为此，首先要根据已知力，应用平衡条件求解，为此，首先要确定构件受了几个力，每个力的作用位置和力要确定构件受了几个力，每个力的作用位置和力要确定构件受了几个力，每个力的作用位置和力要确定构件受了几个力，每个力的作用位置和力的作用方向，这种分析过程称为物体的受力分析。的作用方向，这种分析过程称为物体的受力分析。的作用方向，这种分析过程称为物体的受力分析。的作用方向，这种分析过程称为物体的受力分析。2 2 、选取研究对象、选取研究对象、选取研究对象、选取研究对象 为了清晰地表示物体的的受力情况，我们把需为了清晰地表示物体的的受力情况，我们把需为了清晰地表示物体的的受力情况，我们把需为了清晰地表示物体的的受力情况，我们把需要研究的物体（称为分离体）从周围的物体（称要研究的物体（称为分离体）从周围的物体（称要研究的物体（称为分离体）从周围的物体（称要研究的物体（称为分离体）从周围的物体（称为施力体）中分离出来，单独画出他们的简图，为施力体）中分离出来，单独画出他们的简图，为施力体）中分离出来，单独画出他们的简图，为施力体）中分离出来，单独画出他们的简图，这个步骤叫做取研究对象或取分离体这个步骤叫做取研究对象或取分离体这个步骤叫做取研究对象或取分离体这个步骤叫做取研究对象或取分离体303 3、受力图、受力图、受力图、受力图 选取研究对象后，要把施力物体对研究对象选取研究对象后，要把施力物体对研究对象选取研究对象后，要把施力物体对研究对象选取研究对象后，要把施力物体对研究对象的作用力（包括主动力和约束反力）全部画出的作用力（包括主动力和约束反力）全部画出的作用力（包括主动力和约束反力）全部画出的作用力（包括主动力和约束反力）全部画出来，这种表示物体受力的简明图形，称为受力图来，这种表示物体受力的简明图形，称为受力图来，这种表示物体受力的简明图形，称为受力图来，这种表示物体受力的简明图形，称为受力图 画受力图是解决静力学的一个重要步骤，画受力图是解决静力学的一个重要步骤，画受力图是解决静力学的一个重要步骤，画受力图是解决静力学的一个重要步骤，不能省略，更不能发生错误，否则，将导致以后不能省略，更不能发生错误，否则，将导致以后不能省略，更不能发生错误，否则，将导致以后不能省略，更不能发生错误，否则，将导致以后分析计算上的错误分析计算上的错误分析计算上的错误分析计算上的错误2.3 2.3 物体的受力分析和受力图物体的受力分析和受力图312.3 2.3 物体的受力分析和受力图物体的受力分析和受力图4、画受力图步骤：画受力图步骤：3 3、按约束性质画出所有、按约束性质画出所有约束力约束力1 1、取所要研究物体为研究对象（、取所要研究物体为研究对象（分离体分离体) )2 2、画出所有、画出所有主动力主动力32例例2-12-1解：解：画出简图画出简图画出主动力画出主动力画出约束力画出约束力碾子重为碾子重为 ，拉力为，拉力为 ， 、 处光滑处光滑接触，画出碾子的受力图接触，画出碾子的受力图33例例2-2 2-2 解：取屋架解：取屋架画出主动力画出主动力画出约束力画出约束力画出简图画出简图屋架受均布风力屋架受均布风力 （N/mN/m），）， 屋架重为屋架重为 ，画出屋架的受，画出屋架的受力图力图34例例2-3 2-3 梁梁AB的一端用铰链、另一端用柔的一端用铰链、另一端用柔索固定在墙上，在索固定在墙上，在D处挂一重物，其重量处挂一重物，其重量为为P，梁的自重不计，画出梁的受力图。，梁的自重不计，画出梁的受力图。ADBCABFAxFAyTDPADBGTPFA解：取梁为研究对象解：取梁为研究对象由三力平衡汇交原理由三力平衡汇交原理若考虑梁自重若考虑梁自重WADBFAxFAyTP35例例2-4 2-4 水泥管用两撑架支撑置于斜面水泥管用两撑架支撑置于斜面上，上，A、B、C三处均为光滑铰链，不计三处均为光滑铰链，不计撑架自重，撑架自重，D、E处的摩擦不计。画出处的摩擦不计。画出AC、AB、管子及整体的受力图。、管子及整体的受力图。 ABCDEP3045ACDEPAB解：解：ABCEP成对地作用在系统内成对地作用在系统内,称称为系统的为系统的内约束力内约束力,在受在受力图上不必画出力图上不必画出 36例例2-52-5 不计三铰拱桥的自重与摩擦，不计三铰拱桥的自重与摩擦，画出左、右拱画出左、右拱 的受力图的受力图与系统整体受力图与系统整体受力图解解：CB为二力构件为二力构件37例例2-6 2-6 画出各构件及整体的受力图，画出各构件及整体的受力图，未画重力的物体的重量不计。未画重力的物体的重量不计。解：解：38例例2-72-7不计自重的梯子放在光滑水不计自重的梯子放在光滑水平地面上，画出梯子、梯子平地面上，画出梯子、梯子左右两部分与整个系统受力左右两部分与整个系统受力图图解解：绳子受力图如图（绳子受力图如图（b b）所示）所示39梯子左边部分受力图梯子左边部分受力图如图（如图（c c）所示）所示梯子右边部分受力图梯子右边部分受力图如图（如图（d d）所示）所示40整体受力图如图（整体受力图如图（e e）所示）所示提问：左右两部分梯子在提问：左右两部分梯子在A A处，绳子对左右两部分梯子均有处，绳子对左右两部分梯子均有力作用，为什么在整体受力图没有画出？力作用，为什么在整体受力图没有画出？412.3 2.3 物体的受力分析和受力图物体的受力分析和受力图画受力图应注意画受力图应注意2、不要多画力、不要多画力 要注意力是物体之间的相互机械作用。因此对于受力体所要注意力是物体之间的相互机械作用。因此对于受力体所受的每一个力，都应能明确地指出它是哪一个施力体施加的。受的每一个力，都应能明确地指出它是哪一个施力体施加的。1、不要漏画力、不要漏画力 除重力、电磁力外，物体之间只有通过接触才有相互机械除重力、电磁力外，物体之间只有通过接触才有相互机械作用力，要分清研究对象（受力体）都与周围哪些物体（施力作用力，要分清研究对象（受力体）都与周围哪些物体（施力体）相接触，接触处必有力，力的方向由约束类型而定。体）相接触，接触处必有力，力的方向由约束类型而定。422.3 2.3 物体的受力分析和受力图物体的受力分析和受力图 约束反力的方向必须严格地按照约束的类型来画，不约束反力的方向必须严格地按照约束的类型来画，不能单凭直观或根据主动力的方向来简单推想。在分析两物能单凭直观或根据主动力的方向来简单推想。在分析两物体之间的作用力与反作用力时，要注意，作用力的方向一体之间的作用力与反作用力时，要注意，作用力的方向一旦确定，反作用力的方向一定要与之相反，不要把箭头方旦确定，反作用力的方向一定要与之相反，不要把箭头方向画错。向画错。3、不要画错力的方向、不要画错力的方向4、受力图上不能再带约束。、受力图上不能再带约束。 即受力图一定要画在分离体上。即受力图一定要画在分离体上。438、尺规作图、尺规作图7 、正确判断二力构件，三力汇交原理的运用。、正确判断二力构件，三力汇交原理的运用。2.3 2.3 物体的受力分析和受力图物体的受力分析和受力图 一个力，属于外力一个力，属于外力(external force)还是内力还是内力(internal force) ，因研究对象的不同有可能不同。当物体系统拆开来分析时，因研究对象的不同有可能不同。当物体系统拆开来分析时，原系统的部分内力，就成为新研究对象的外力。原系统的部分内力，就成为新研究对象的外力。 对于某一处的约束反力的方向一旦设定，在整体、局部对于某一处的约束反力的方向一旦设定，在整体、局部或单个物体的受力图上要与之保持一致。或单个物体的受力图上要与之保持一致。 5、受力图上只画外力，不画内力。、受力图上只画外力，不画内力。 6 、同一系统各研究对象的受力图必须整体与局部一致，相、同一系统各研究对象的受力图必须整体与局部一致，相 互协调，不能相互矛盾。互协调，不能相互矛盾。442.4 2.4 共点力的合成共点力的合成共点共点力系力系(concurrent force system) 所有力的作用线汇交于一点的力系称为共点力系，又叫汇交所有力的作用线汇交于一点的力系称为共点力系，又叫汇交力系。力系。 空间汇交力系空间汇交力系452.4 2.4 共点力的合成共点力的合成平面汇交力系平面汇交力系462.4 2.4 共点力的合成共点力的合成一、共点力合成的几何法一、共点力合成的几何法 共点力（汇交力系）可简化为一共点力（汇交力系）可简化为一合力合力，合力为各分力，合力为各分力的矢量和，的矢量和，作用线通过各力的交点作用线通过各力的交点。F1+F2F1+F2+F3平行四边形法则平行四边形法则472.4 2.4 共点力的合成共点力的合成F1+F2F1+F2+F3力多边形法则力多边形法则 把各力矢首尾相接，形成一条有向折线段（称为力链）。把各力矢首尾相接，形成一条有向折线段（称为力链）。加上一封闭边，就得到一个多边形，称为力多边形。加上一封闭边，就得到一个多边形，称为力多边形。 合力矢是力多边形的封闭边，这种求合力的方法成为力合力矢是力多边形的封闭边，这种求合力的方法成为力多边形法。多边形法。 注意：在力多边形中，各分力矢首尾相接，环绕同一方注意：在力多边形中，各分力矢首尾相接，环绕同一方向，而合力矢则反向封闭力多边形。向，而合力矢则反向封闭力多边形。482.4 2.4 共点力的合成共点力的合成二、力的投影与解析表达式二、力的投影与解析表达式投影：投影：分力：分力： 若已知力在直角坐标系若已知力在直角坐标系Oxyz的投影，则力的投影，则力 F 的大小：的大小：方向余弦为方向余弦为 ： 492.4 2.4 共点力的合成共点力的合成间接投影法（二次投影法）间接投影法（二次投影法） 若已知力与某轴的夹角，若已知力与某轴的夹角， 在力与轴组成的平面内将力沿轴及与轴垂直的方向分解，在力与轴组成的平面内将力沿轴及与轴垂直的方向分解， 分力的大小为：分力的大小为：若若在在xy内的方向可以确定，则投影为：内的方向可以确定，则投影为：注意：注意：力在轴上投影是代数值。力在轴上投影是代数值。力在平面上的投影是矢量力在平面上的投影是矢量。502.4 2.4 共点力的合成共点力的合成对平面力系对平面力系 力的投影为力的投影为力的解析表达式为力的解析表达式为力力 F的大小和方向余弦可表示为的大小和方向余弦可表示为512.4 2.4 共点力的合成共点力的合成三、共点力合成的解析法三、共点力合成的解析法(a)(a)A AF F2 2F F1 1F F3 3F F1 1F F2 2F FR RF F3 3x xA AB BC CD D(b)(b) 合力在任一轴上的投影，等于它的各分力在同一轴上的合力在任一轴上的投影，等于它的各分力在同一轴上的投影的代数和。投影的代数和。证明：以三个力组成的共点力系为例。证明：以三个力组成的共点力系为例。 设有三个共点力设有三个共点力F1、F2、F3 如图。如图。合矢量投影定理：合矢量投影定理： 522.4 2.4 共点力的合成共点力的合成合力合力 FR 在在x 轴上投影：轴上投影：F F1 1F F2 2F FR RF F3 3x xA AB BC CD D(b)(b) 推广到任意多个力推广到任意多个力F1、F2、 Fn 组成的组成的共点力系，共点力系，可得：可得：a ab bc cd d各力在各力在x 轴上投影：轴上投影：532.4 2.4 共点力的合成共点力的合成共点力合成的解析法共点力合成的解析法由合矢量投影定理，有由合矢量投影定理，有FRx 、 FRy、 FRz、为合力、为合力FR在在x、y 、z轴上的投影轴上的投影 则合力为则合力为542.4 2.4 共点力的合成共点力的合成对平面汇交力系对平面汇交力系,合力可表示为合力可表示为合力的大小和方向余弦为合力的大小和方向余弦为 汇交力系的合力等于各分力的矢量和，合力的作用线汇交力系的合力等于各分力的矢量和，合力的作用线通过汇交点通过汇交点.55例例 2-7 圆柱斜齿轮，其上受啮合力圆柱斜齿轮，其上受啮合力F作用。已知斜齿轮的作用。已知斜齿轮的齿倾角（螺旋角）齿倾角（螺旋角）和压力角和压力角 ，试求力，试求力F在各轴上的投影。在各轴上的投影。 Fy解：先将力解：先将力F沿沿z轴和轴和Oxy平面分解，得平面分解，得再将力再将力Fxy向向x、y轴的投影，有轴的投影，有56例例2-8 求平面汇交力系的合力。求平面汇交力系的合力。解：一、求各力投影解：一、求各力投影57二、求合力大小二、求合力大小FRyFRx58三、求合力的方向三、求合力的方向合力FR在第二象限。FRyFRxR592.4 2.4 力对点的矩和力对轴的矩力对点的矩和力对轴的矩一、力对点的矩一、力对点的矩力对点的矩是力使物体绕某点转动效应的度量。力对点的矩是力使物体绕某点转动效应的度量。 (1) (1) 矩心矩心(2)(2)力力F、力臂、力臂力臂：矩心到力作用线的距离力臂：矩心到力作用线的距离602.4 2.4 力对点的矩和力对轴的矩力对点的矩和力对轴的矩方向由右手螺旋法则确定方向由右手螺旋法则确定常用单位常用单位Nm或或kNm力对点之矩的矢量定义式力对点之矩的矢量定义式设矩心设矩心O到力到力 的作用点的作用点K的矢径为的矢径为 ，则定义力，则定义力 对矩心对矩心O点的矩矢量为：点的矩矢量为：612.4 2.4 力对点的矩和力对轴的矩力对点的矩和力对轴的矩则力对点的矩可表示为则力对点的矩可表示为力对点的矩矢量大小和方向都与矩心的位置有关力对点的矩矢量大小和方向都与矩心的位置有关定位矢量定位矢量 622.4 2.4 力对点的矩和力对轴的矩力对点的矩和力对轴的矩平面力对其作用面内一点的力矩是平面力对其作用面内一点的力矩是空间力矩矢量的退化形式。空间力矩矢量的退化形式。d为力臂。为力臂。平面力对其作用面内一点的矩大小：平面力对其作用面内一点的矩大小：因平面中只有顺逆时针两个转动方向，所以，只需正负两个因平面中只有顺逆时针两个转动方向，所以，只需正负两个符号即可确定转向。符号即可确定转向。所以，平面中力对点的矩为：所以，平面中力对点的矩为：是代数量。是代数量。-+632.4 2.4 力对点的矩和力对轴的矩力对点的矩和力对轴的矩二、共点力的合力矩定理二、共点力的合力矩定理若力系存在合力，则合力对某一点的力矩等于各分若力系存在合力，则合力对某一点的力矩等于各分力对同一点力矩的矢量和。可表示为力对同一点力矩的矢量和。可表示为证明：证明：642.4 2.4 力对点的矩和力对轴的矩力对点的矩和力对轴的矩三、力对轴的矩三、力对轴的矩 力使物体绕固定轴转动效应的度量力使物体绕固定轴转动效应的度量（1 1）力使扳手绕）力使扳手绕z轴转动轴转动 转动效应与力的大小及转动效应与力的大小及dy有关，取决于力在有关，取决于力在Oxy平面内平面内 对对O点的矩。点的矩。 （2 2）力与）力与z z轴相交或与轴平行无绕轴的转动效果轴相交或与轴平行无绕轴的转动效果652.4 2.4 力对点的矩和力对轴的矩力对点的矩和力对轴的矩Def 力对轴的矩力对轴的矩为力在垂直于轴平面为力在垂直于轴平面内的分力对轴与该平面交点的力矩内的分力对轴与该平面交点的力矩。也可先将力分解，利用合力矩定理也可先将力分解，利用合力矩定理求力对轴的矩求力对轴的矩 FxFyxyz zOFFxFyF z(x，y，z) A Axyz正负按右手法则正负按右手法则( (大拇指与大拇指与Z Z轴正方向轴正方向同向时为正同向时为正) )。662.4 2.4 力对点的矩和力对轴的矩力对点的矩和力对轴的矩四、力对点的矩和力对轴的矩的关系四、力对点的矩和力对轴的矩的关系 力对点的矩在过这点的轴上的投力对点的矩在过这点的轴上的投影等于力对这轴的矩，即影等于力对这轴的矩，即67例例2-10 2-10 如图所示圆柱形直齿轮，受啮合力如图所示圆柱形直齿轮，受啮合力F的作用，压力的作用，压力角为角为，齿轮节圆半径为，齿轮节圆半径为r，计算力，计算力F对对O点的力矩。点的力矩。xy解解: :直接按定义直接按定义按合力矩定理按合力矩定理由解析表达式由解析表达式68例例2-11 已知已知:P=2kN, C点在点在Oxy平面内。求：力平面内。求：力P对三个坐标轴对三个坐标轴的矩。的矩。解：解：1、计算分力大小、计算分力大小692、合力矩定理计算力对轴的矩、合力矩定理计算力对轴的矩3、也可以将、也可以将C点坐标及力的投影代入公式计算点坐标及力的投影代入公式计算702.6 2.6 力偶力偶1 1、力偶力偶由两个等值、反向、不共由两个等值、反向、不共线的（平行）力组成的力系线的（平行）力组成的力系一、力偶与力偶矩一、力偶与力偶矩力偶是力偶是静力学的基本要素之一静力学的基本要素之一2 2、力偶矩力偶矩力偶对物体的转动效应力偶对物体的转动效应 （1 1） 大小：力与力偶臂；大小：力与力偶臂；（3 3） 作用面：力偶作用面。作用面：力偶作用面。 （2 2） 方向：转动方向；方向：转动方向；712.6 2.6 力偶力偶 Def力偶矩矢量力偶矩矢量自由矢量自由矢量若问题涉及的力偶的作用面共面或平行，力偶矩可用标量表示为若问题涉及的力偶的作用面共面或平行，力偶矩可用标量表示为 -+FFdM722.6 2.6 力偶力偶一、力偶的性质一、力偶的性质性质性质1 力偶的矢量和为零，但不能相互平衡，是一种非零的力偶的矢量和为零，但不能相互平衡，是一种非零的最简单力系。最简单力系。性质性质2 力偶对刚体的作用效果完全取决于力偶矩矢量。力偶对刚体的作用效果完全取决于力偶矩矢量。推论：推论：只要保持偶矩矢量不变，力偶可在作用面内任意移动只要保持偶矩矢量不变，力偶可在作用面内任意移动或转动，或同时改变力和力偶臂的大小，或将其作用面平行或转动，或同时改变力和力偶臂的大小，或将其作用面平行移动，它对刚体的作用效果不变。移动，它对刚体的作用效果不变。732.6 2.6 力偶力偶三、力偶系的合成三、力偶系的合成 可以证明，任意个空间分布的力偶可以合成为一个力偶，可以证明，任意个空间分布的力偶可以合成为一个力偶，合力偶矩矢等于各分力偶矩矢的矢量和，因而可用矢量求和合力偶矩矢等于各分力偶矩矢的矢量和，因而可用矢量求和法则求和力偶矩矢，即法则求和力偶矩矢，即对于平面力偶系对于平面力偶系 74