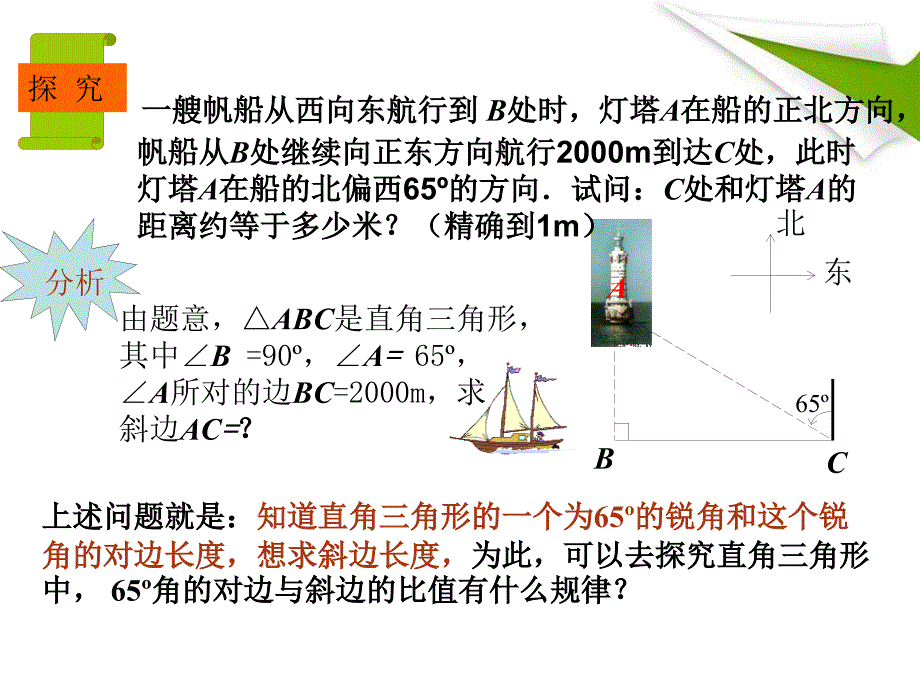
4.1 4.1 正弦和余弦正弦和余弦第第1 1课时课时 正弦及正弦及3030角的正弦值角的正弦值 分析由题意，ABC是直角三角形， 其中B =90，A= = 65，A所对的边BC=2000m，求 斜边AC= =？北东上述问题就是：上述问题就是：知道直角三角形的一个为知道直角三角形的一个为65的锐角和这个锐的锐角和这个锐角的对边长度，想求斜边长度，角的对边长度，想求斜边长度，为此，可以去探究直角三角形为此，可以去探究直角三角形中，中， 65角的对边与斜边的比值有什么规律？角的对边与斜边的比值有什么规律？65ABC 一艘帆船从西向东航行到一艘帆船从西向东航行到 B处时，灯塔处时，灯塔A在船的正北方向，在船的正北方向，探 究帆船从帆船从B处继续向正东方向航行处继续向正东方向航行2000m到达到达C处，此时处，此时灯塔灯塔A在船的北偏西在船的北偏西65的方向试问：的方向试问：C处和灯塔处和灯塔A的的距离约等于多少米？（精确到距离约等于多少米？（精确到1m）每位同学画一个直角三角形，其中一个锐每位同学画一个直角三角形，其中一个锐角为角为65 ，量出，量出65角的对边长度和斜边长角的对边长度和斜边长度，计算：度，计算：的值的值，结论：结论：在有一个锐角为在有一个锐角为65的直角三角形中，的直角三角形中， 65角的对边与角的对边与斜边的比值是一个常数，它约等于斜边的比值是一个常数，它约等于0.91做一做做一做与同桌和邻近桌的同学交流，计算出与同桌和邻近桌的同学交流，计算出的比值是否相等（精确到的比值是否相等（精确到0.010.01）？）？结论证明结论证明 已知：任意两个直角三角形已知：任意两个直角三角形DEF和和DEF，D =D =65，E =E= 90,求证：求证：DEFDEF E =E = 90，D =D =65， DEF DEF 证明：证明：因此在有一个锐角为因此在有一个锐角为6565的所有直角三角形中，的所有直角三角形中， 6565角角的对边与斜边的比值是一个常数的对边与斜边的比值是一个常数于是于是E F D F E F D F 解决问题解决问题现在解决帆船航行到现在解决帆船航行到C处时和灯塔处时和灯塔A的距的距离约等于多少米的问题离约等于多少米的问题解解在直角三角形在直角三角形ABC中中，BC=2000m ，A= 65，解得解得在直角三角形中，在直角三角形中，锐角锐角的对边与斜边的比的对边与斜边的比叫做叫做角角的正的正弦弦，记作，记作:类似地可以证明：类似地可以证明：在有一个锐角等于在有一个锐角等于的所有直角三的所有直角三角形中，角角形中，角的对边与斜边的比值为一个的对边与斜边的比值为一个常数常数即即:定义定义 在直角三角形在直角三角形ABC中，中， C= 90， BC=3，AB=5（）求（）求A的正弦的正弦 ；（）求（）求B的正弦的正弦 （）（） A的对边的对边BC=3，斜边斜边 AB=5于是于是（）（） B的对边是的对边是AC根据勾股定理，得根据勾股定理，得于是于是AC=4因此因此CAB35例例 题题解解1 1在直角三角形在直角三角形ABC中，中， C= 90， BC=5，AB=13（）求（）求 的值；的值；（）求的值（）求的值2小刚说：对于任意锐角小刚说：对于任意锐角，都有，都有你认为他说得对吗？为什么？你认为他说得对吗？为什么？0 1CAB513练练 习习我认为他说得对，因为正弦值是相对直角三角形来说的，而在直角三角形中直角边比斜边小，所以直角边与斜边的比值小于1，又因为直角边和斜边的长度值都是正数，所以直角边与斜边的比值大于0.在直角三角形中，在直角三角形中，小结小结在直角三角形中，在直角三角形中，3030角所对的直角边与斜边角所对的直角边与斜边有什么关系？有什么关系？说一说说一说1在在Rt ABC 中，中， C= 90， BC=5，AB=6求，的值求，的值2在在Rt ABC 中，中， C= 90， BC=7，B=8求求的值的值6BCA5BCA87做一做答案：答案：答案：答案：