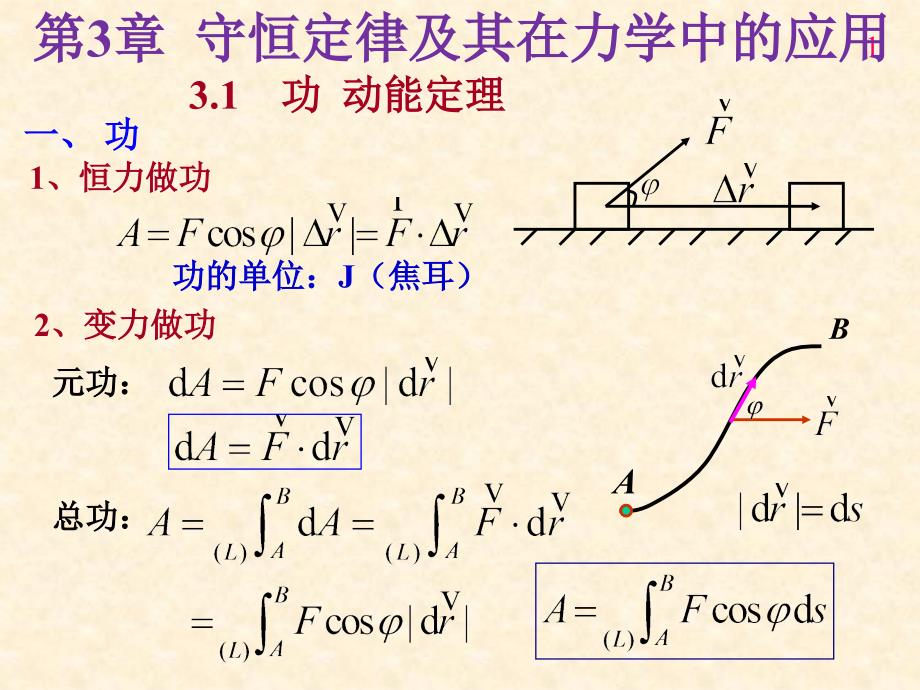
1第第3章章 守恒定律及其在力学中的应用守恒定律及其在力学中的应用3.1功功 动能定理动能定理1、恒力做功、恒力做功2、变力做功、变力做功元功：元功：总功：总功：AB一、一、 功功 功的单位：功的单位：J（焦耳）（焦耳） 直角坐标系下的功直角坐标系下的功:例例 已知力已知力质点从原点移动到质点从原点移动到x = 8, y = 6处该力做功多少处该力做功多少?ABoyxz33、合力的功、合力的功4、功率、功率 功率的单位：功率的单位：W（瓦）（瓦） 1 W = 1 Js- -1 合外力对物体所做的功等于各分力沿同一路径所做功的代数和合外力对物体所做的功等于各分力沿同一路径所做功的代数和平均功率平均功率瞬时功率瞬时功率4由由代入上式代入上式因为：因为：1. 质点动能质点动能或或2. 质点的动能定理质点的动能定理二、质点的动能定理二、质点的动能定理三、质点系动能定理三、质点系动能定理n个质点组成的质点系：个质点组成的质点系：m1:对每个质点分别使用动能定理对每个质点分别使用动能定理m2:mn:注意：注意：内力内力能否能否改变系统的改变系统的总动能总动能？质点系的动能定理质点系的动能定理6相互作用的两个质点相互作用的两个质点m1和和m2作用力作用力 和反作用力和反作用力做功之和是否为做功之和是否为0？OA1B1A2B2m1m2两个质点间的两个质点间的“一对力一对力”做功之和等于其中一个质点受的做功之和等于其中一个质点受的力力沿着该质点相对于另一质点所移动的路径所做的功。沿着该质点相对于另一质点所移动的路径所做的功。一对力的功一对力的功系统内力系统内力光滑光滑光滑光滑光滑光滑作用力作用力 做功是否为做功是否为0？做功之和是否为做功之和是否为0？反作用力反作用力 做功是否为做功是否为0？3.2 保守力保守力 系系统的的势能势能 一、保守力做功的特点一、保守力做功的特点1. 重力做功重力做功 重力做功与路径无关重力做功与路径无关xyoaby1y2也可写成也可写成为单位矢量为单位矢量ALL2.2. 万有引力做功万有引力做功101. 任意两点间做功与路径无关任意两点间做功与路径无关, 即即L1ABL22. 沿任意闭合回路做功为沿任意闭合回路做功为 0. 即即沿任意回路做功为零的沿任意回路做功为零的力力或做功与具体路径无关的或做功与具体路径无关的力力都称为都称为保守力保守力Ox1x2xk保守力保守力3. 弹簧的弹性力做功弹簧的弹性力做功保守力一般判断：保守力一般判断： 1，一维运动，一维运动 ， 力是位置的单值函数力是位置的单值函数 弹性力弹性力万有引力万有引力2，一维以上运动，一维以上运动 ，大小，方向都和位置无关的力，大小，方向都和位置无关的力 重力重力3，有心力，有心力 空间存在一个中心空间存在一个中心 O,物体在任何位置上受力沿物体在任何位置上受力沿的正负方向，大小是的正负方向，大小是r 的函数的函数12保守力作功表现为一种位置函数的负增量保守力作功表现为一种位置函数的负增量. 若选若选 B 为计算势能参考点为计算势能参考点, 取取EpB = 0势能势能相对量相对量: :相对于势能零点的相对于势能零点的系统量系统量: :是属于相互作用的质点共有的是属于相互作用的质点共有的(沿任意路径）沿任意路径）(沿任意路径）沿任意路径）系统在任一位置时的势能等于它从此位置系统在任一位置时的势能等于它从此位置沿任意路径沿任意路径改变至改变至势能零点时保守力所做的功。势能零点时保守力所做的功。势能定义势能定义势能与参考系无关势能与参考系无关(相对位移相对位移)二、势能二、势能13 引力势能引力势能:选选 处为零势点处为零势点弹性势能弹性势能:重力势能重力势能: 引力势能引力势能弹性势能弹性势能重力势能重力势能选选 弹簧自然伸长位置为零势点弹簧自然伸长位置为零势点选选 y=0处处为零势点为零势点14 引力势能引力势能:弹性势能弹性势能:重力势能重力势能:引力引力弹性力弹性力重力重力三三. .保守力与势能的关系保守力与势能的关系m15在直角作标系中在直角作标系中保守力等于保守力等于势能的负梯度势能的负梯度3.33.3 质点质点系系的的功能定理功能定理 机械能守恒定律机械能守恒定律 能量守恒能量守恒由质点系动能定理由质点系动能定理因为因为所以所以机械能机械能 质点系的功能原理质点系的功能原理一、一、质点系质点系的功能定理的功能定理17机械能守恒定律机械能守恒定律一个质点系在运动中，当只有保守内力做功一个质点系在运动中，当只有保守内力做功 时，系统的机械能保持不变时，系统的机械能保持不变二、机械能守恒定律二、机械能守恒定律18保守内力作功：相应势能和保守内力作功：相应势能和系统动能系统动能系统动能系统动能间转换；间转换；所以所以A保内保内是是Ep与与Ek之间转化的手段和量度。之间转化的手段和量度。19非保守内力作功：系统机械能与非保守内力作功：系统机械能与内部其他形式内部其他形式内部其他形式内部其他形式 能量间转换。能量间转换。 若若A内非内非 0, 它的机械能就不守恒。它的机械能就不守恒。 A内非内非 0 ， E2 E1-其他形式能量转化为机械能其他形式能量转化为机械能 (地雷）地雷） A内非内非 0 ，E2 E1-机械能转化为其他形式能量机械能转化为其他形式能量 （摩擦）（摩擦）外力的功：系统机械能与外力的功：系统机械能与外界外界外界外界能量的交换或转换能量的交换或转换三、三、能量守恒定律能量守恒定律一个孤立系统经历任何变化时，该系统所有一个孤立系统经历任何变化时，该系统所有能量的总和保持不变能量的总和保持不变普遍的能量守恒定律普遍的能量守恒定律功功和和能量的变化能量的变化相联系相联系，能量的变化能量的变化反映了系统反映了系统作功的本领。作功的本领。能量是运动状态的单值函数：和状态的一一对应性。能量是运动状态的单值函数：和状态的一一对应性。从普遍能量守恒观点：从普遍能量守恒观点： 功是能量传递或转换的一种度量！功是能量传递或转换的一种度量！功是能量传递或转换的一种度量！功是能量传递或转换的一种度量！即：能量只能传递或转换，而不能创生。即：能量只能传递或转换，而不能创生。例：如图，求绳全部离开光滑桌面时的瞬时速率例：如图，求绳全部离开光滑桌面时的瞬时速率t t =0=0，v=0=0M M，L Lb bx xo o解：解：利用动能定理利用动能定理由动能定理得：由动能定理得：建立作坐标系，重力所作元功为：