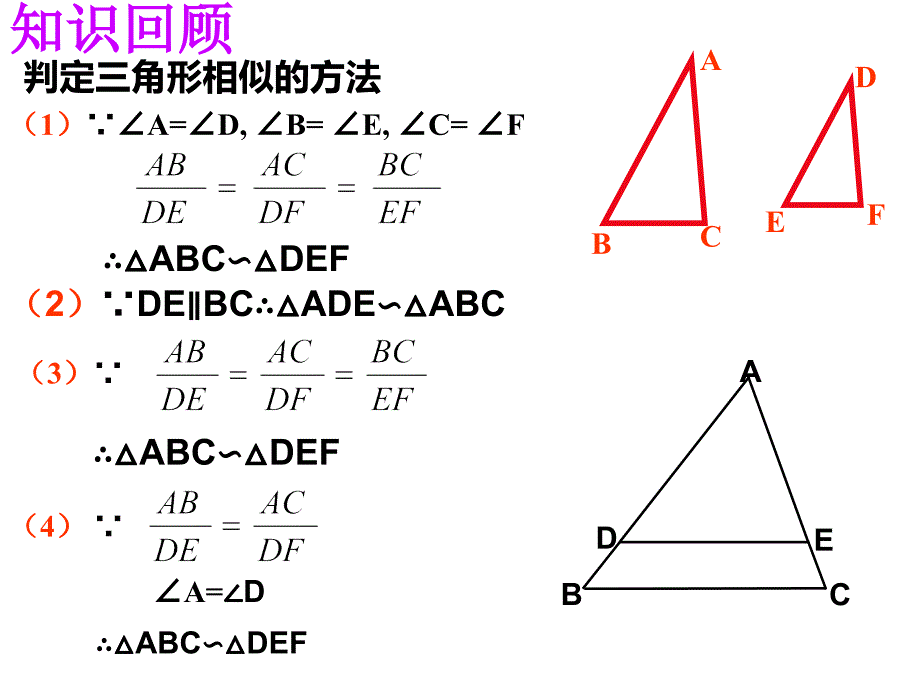
DBACE（2）DE BCADEABC判定三角形相似的方法知识回顾知识回顾ACBEDF（1）A=D, B= E, C= FABCDEF（3）ABCDEF（4） A= DABCDEF观察 观察两副三角尺，其中同样角度（观察两副三角尺，其中同样角度（30与与60，或，或45与与45）的两个三角尺）的两个三角尺,它们一定相它们一定相似吗？似吗？ 如果两个三角形有两组角对应相等，如果两个三角形有两组角对应相等，它们一定相似吗？它们一定相似吗？ABCA/ C/ B/ 已知：在已知：在ABC 和和ABC中中, A= A,B= B求证：求证： ABC ABC证明：在证明：在ABC的边的边AB、AC上，分别截取上，分别截取AD=A/B/,AE=A/C/，连结连结DE。ABCA/ C/ B/ P46 P46 判定定理判定定理判定定理判定定理3 3：如果一个三角形的两个角与另一个三角形的如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似。两个角对应相等，那么这两个三角形相似。可以简单说成：两角对应相等，两三角形相似。两角对应相等，两三角形相似。D E AD=A/B/,A=A/，AE=A/C/ A DE A/B/C/（SAS） ADE=B/，又又 B/=B， ADE=B， DE/BC， ADEABC。 A/B/C/ABC已知：在已知：在ABC ABC 和和 A AB BC C, ,中中, ,-“两角两角”定理定理 A=A， B=B ABC ABC符号语言：符号语言：CAABBC相似三角形判定定理相似三角形判定定理3 3：如果一个三角形的如果一个三角形的两个角两个角与另一个三角形的与另一个三角形的两个两个角角对应相等对应相等，那么这两个三角形，那么这两个三角形相似相似. .简单说成：简单说成：两角两角对应对应相等相等，两三角形，两三角形相似相似.相似三角形判定方法相似三角形判定方法1、(定义)三组对应边的比相等且对应角相等；3、（判定定理1）三组对应边的比相等的两个三角形相似。2、（平行）平行于三角形一边的直线与其他两边(或两边的延长线)相交，所构成的三角形与原三角形相似。4、（判定定理2）两组对应边之比相等且夹角相等的两个三角形相似。5、（判定定理3）两角对应相等的两个三角形相似。ABCABC基础演练1、下列图形中两个三角形是否相似？ABCDEABCACBABCDE(1)(2)(3)(4)如图,弦AB和CD相交于O内一点P,求证:PAPB=PCPDODPCBA例题讲解例题讲解例题讲解例题讲解变式：如果弦AB和CD相交于圆O外一点P，结论还成立吗？变式：上题中，重合为一点时，PA与圆O相切，又会有什么结论？OO1、判断题：所有的直角三角形都相似.（）所有的等边三角形都相似.（）所有的等腰直角三角形都相似.（）有一个角相等的两等腰三角形相似.（）顶角相等顶角相等底角相等底角相等顶角与底角相等顶角与底角相等BCAABC第第一一种种情情况况 ABC ABC顶角相等顶角相等BCAABC第第二二种种情情况况 ABC ABC底角相等底角相等第第三三种种情情况况ABCABC两三角形不相似顶角与底角相等顶角与底角相等1、已知如图直线BE、DC交于A，E=C求证：DAAC=ABAEDEABC C证明：证明： E=C DAE=BAC ABC ADE AC :AE=AB :AD DA AC=AB AE2、已知如图直线BE、DC交于A，DAAC=ABAE求证：E= CADEBC CEADC C如何证明如何证明DEA= CBEADC CBBEADC C解：解： A= A ABD=C ABD ACB AB : AC=AD : AB AB2 = AD AC AD=2 AC=8 AB =43.已知如图，ABD=CAD=2，AC=8，求ABABC CDABDC CABDC C4 4、如图：在、如图：在RtRt ABC ABC中，中， ABC=90ABC=900 0，BDACBDAC于于D D 问：图中有几个直角三角形？它们相似吗？为什么？问：图中有几个直角三角形？它们相似吗？为什么？解：解： 图中有三个直角三角形，分别是：图中有三个直角三角形，分别是： ABC、 ADB、 BDC ABC ADB BDC 5、求证：直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。ADBC已知：在RtABC中，CD是斜边AB上的高。此结论可以称为“母子相似定理母子相似定理”求证：ABCACDCBD结论： ACD CBD CD2=AD DB ACD ABC AC2=AD AB BCD ABC BC2=BD ABP49练习练习2DBC CA如图：在如图：在Rt ABC中，中， ABC=900，BDAC于于D 若若 AB=6 AD=2 则则AC= BD= BC= 184 2122相似三角形判定方法相似三角形判定方法1、(定义)三组对应边的比相等且对应角相等；3、（判定定理1）三组对应边的比相等的两个三角形相似。2、（平行）平行于三角形一边的直线与其他两边(或两边的延长线)相交，所构成的三角形与原三角形相似。4、（判定定理2）两组对应边之比相等且夹角相等的两个三角形相似。5、（判定定理3）两角对应相等的两个三角形相似。ABCDE1已知DEBC且1=B，则图中共有对相似三角形。 DEBCADEABC 1=B ，A=A ACDABCADE ACD DEBC EDC=DCB， 又又 1=BDECCDB4