资源预览内容
space
第1页 / 共156页
space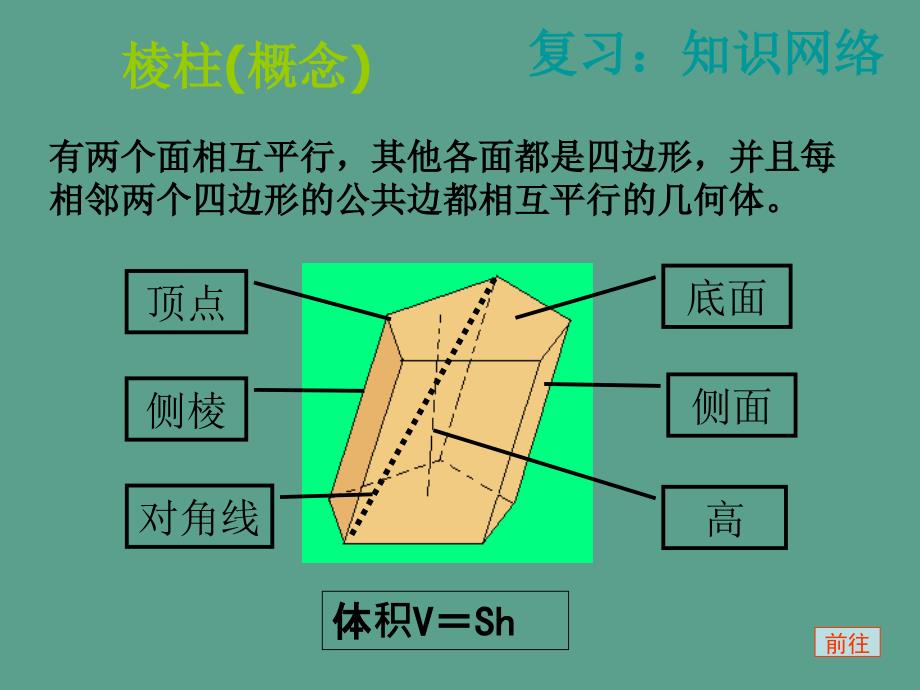
第2页 / 共156页
space
第3页 / 共156页
space
第4页 / 共156页
space
第5页 / 共156页
space
第6页 / 共156页
space
第7页 / 共156页
space
第8页 / 共156页
space
第9页 / 共156页
space
第10页 / 共156页
亲,该文档总共156页,到这儿已超出免费预览范围,如果喜欢就下载吧!
资源描述
棱柱问题棱锥问题复习:知识网络复习:知识网络底面对角线高侧面侧棱顶点棱柱棱柱(概念概念)有两个面相互平行,其他各面都是四边形,并且每有两个面相互平行,其他各面都是四边形,并且每相邻两个四边形的公共边都相互平行的几何体。相邻两个四边形的公共边都相互平行的几何体。体体积V VShSh前往复习:知识网络复习:知识网络棱柱棱柱(分类分类)棱棱柱柱斜棱柱斜棱柱直棱柱直棱柱正棱柱正棱柱前往复习:知识网络复习:知识网络四棱柱四棱柱四棱柱四棱柱直四棱柱直四棱柱侧棱垂直底面侧棱垂直底面平行六面体平行六面体底面是平行四边形底面是平行四边形长方体长方体正四棱柱正四棱柱正方体正方体侧面垂直面垂直底面底面前往要点要点疑点疑点考点考点一、棱柱一、棱柱(1)有有两两个个面面相相互互平平行行,其其他他各各面面都都是是四四边形形,并并且且每每相相邻两两个个四四边形形的的公公共共边都都相相互互平平行行,由由这些些面面围成成的几何体叫棱柱的几何体叫棱柱 1.概念概念(2)侧棱棱不不垂垂直直于于底底面面的的棱棱柱柱叫叫斜斜棱棱柱柱,侧棱棱垂垂直直于于底底面面的的棱棱柱柱叫叫直直棱棱柱柱,底底面面是是正正多多边形形的的直直棱棱柱柱叫叫正正棱棱柱柱 前往(2)两个底面与平行于底面的截面是全等的多两个底面与平行于底面的截面是全等的多边边形;形;2.性性质质(3)过不相不相邻的两条的两条侧棱的截面是平行四棱的截面是平行四边形形.(1)侧侧棱都相等,棱都相等,侧侧面是平行四面是平行四边边形;形;要点要点疑点疑点考点考点3.长长方体及其相关概念、性方体及其相关概念、性质质(1)概念:底面是平行四概念:底面是平行四边形的四棱柱叫平行六面体形的四棱柱叫平行六面体.侧棱与底面垂直的平行六面体叫直平行六面体棱与底面垂直的平行六面体叫直平行六面体.底面是矩形的直平行六面体叫底面是矩形的直平行六面体叫长方体方体.棱棱长都相等的都相等的长方体叫正方体方体叫正方体.(2)性性质:设长方体的方体的长、宽、高分、高分别为a、b、c, 对角角线长为l ,那么,那么l2=a2+b2+c2前往复习:知识网络复习:知识网络棱锥棱锥棱锥棱锥正四棱锥正四棱锥正三棱锥正三棱锥正四面体正四面体体体积V VSh/3Sh/3顶点在底面正多边形的射影是底面的中心前往1.一个三棱一个三棱锥,假,假设它的底面是直角三角形,它的底面是直角三角形,那么它的三个那么它的三个侧面面( )(A)至多只需一个是直角三角形至多只需一个是直角三角形(B)至多只需两个是直角三角形至多只需两个是直角三角形(C)能能够都是直角三角形都是直角三角形(D)必然都是非直角三角形必然都是非直角三角形C根底根底题例例题前往根底根底题例例题2.正三棱柱正三棱柱ABC-A1B1C1中,假中,假设AB=2 BB1,那,那么么AB1与与C1B所成角的大小是所成角的大小是 A.60o B.90o C.105o D.75oB前往3.长方方体体三三边之之和和为a+b+c=6,总面面积为11,那那么么其其对角角线长为_;假假设一一条条对角角线与与二二个个面面所所成成的的角角 为 30或或 45, 那那 么么 与与 另另 一一 个个 面面 所所 成成 的的 角角 为_;假假设一一条条对角角线与与各各条条棱棱所所成成的的角角为、,那么,那么sin、sin、sin的关系的关系为_.sin2+sin2+sin2=2根底根底题例例题530前往才干才干思想思想方法方法4. 在底面是直角梯形的四棱在底面是直角梯形的四棱锥P-ABCD中,中,侧 棱棱 PA底底 面面 ABCD, ABC=90, PA=AB=BC=2,AD=1, (1)求求D到平面到平面PBC的的间隔;隔; (2)求面求面PAB与面与面PCD所成的二面角的大小。所成的二面角的大小。APDCB解解: (1)AD/平面平面PBCD到平面到平面PBC的的间隔等于隔等于A到到平面平面PBC的的间隔隔PABC, ABBCBC平面平面PAB平面平面PBC平面平面PABA到到PB的的间隔就是隔就是A到平面到平面PBC的的间隔隔PA=AB=2, PAAB,A到到PB的的间隔隔为D到平面到平面PBC的的间隔隔为前往才干才干思想思想方法方法4. 在底面是直角梯形的四棱在底面是直角梯形的四棱锥P-ABCD中,中,侧 棱棱 PA底底 面面 ABCD, ABC=90, PA=AB=BC=2,AD=1, (1)求求D到平面到平面PBC的的间隔;隔; (2)求面求面PAB与面与面PCD所成的二面角的大小。所成的二面角的大小。APDCBQ (2)延伸延伸CD与与BA相交于相交于Q,ADBC,且且 AD= BCA是是QB的中点的中点,又又PA=AB=AQBQPQ,又又BC平面平面PAB,CPPQ,故故CPB是所求二面角的是所求二面角的平面角平面角,故面故面PCD与面与面PCD所成的二面角所成的二面角为前往例题讲解例题讲解1 1、四棱、四棱锥P-ABCDP-ABCD的底面是的底面是边长为a a的正方形,的正方形,PBPB面面ABCD.ABCD.(1)(1)假假设面面PADPAD与面与面ABCDABCD的二面角的二面角为600600,求四棱,求四棱锥的体的体积;作、作、 证、 求?求?APDCB PB PB面面ABCDABCD,BAADBAAD,PAADPAADPABPAB就是面就是面PADPAD与面与面ABCDABCD的二面角的平面角的二面角的平面角解:解:即即PABPAB600600在在RtPABRtPAB中,中,ABABa a, PAB PAB600600PBPBa aV= a3V= a3前往例题讲解例题讲解1 1、四棱、四棱锥P-ABCDP-ABCD的底面是的底面是边长为a a的正方形,的正方形,PBPB面面ABCD.ABCD.(2)(2)证明不明不论高高PBPB怎怎样变化,面化,面PADPAD与与面面PCDPCD所成的二面角恒大于所成的二面角恒大于900.900.APDCBM证:由:由题设侧面面PADPAD与与PCDPCD为全等全等,作作CMPDCMPD于于M M,连结MAMA,那么,那么CDMADMCDMADM,AMAMCMCM,AMDAMD900900故故AMCAMC就是所就是所证二面角的平面角二面角的平面角. .连结ACAC在在AMCAMC中,由余弦定理中,由余弦定理cosAMC =cosAMC =故故AMCAMC900900,即,即证. .小小结:作二面角平面角的方法:作二面角平面角的方法有面的垂有面的垂线,那么一作一,那么一作一连法法定定义法,在两面内作棱的垂法,在两面内作棱的垂线面面积射影定理射影定理前往变化一变化一 四棱四棱锥P-ABCDP-ABCD的底面是的底面是边长为a a的菱形,的菱形,BCDBCD600600,PBPB面面ABCD.ABCD.假假设面面PADPAD与面与面ABCDABCD的二面角的二面角为600600,求四棱,求四棱锥的体的体积;APDCBE前往四棱四棱锥P-ABCDP-ABCD的底面是的底面是边长为a a的菱形,的菱形,BCDBCD600600,面,面PBCPBC面面ABCDABCD,且,且PBCPBC是等是等边. . 求求侧面面PADPAD与底面与底面ABCDABCD所成的二面角;所成的二面角;APDCB变化二变化二E留意:留意:面面垂直的运面面垂直的运用用分析平面分析平面图形形前往例题讲解例题讲解2 2、如、如图在直三棱柱在直三棱柱ABC-A1B1C1ABC-A1B1C1中,底面中,底面ABCABC是等腰是等腰RtRt, C=900 C=900 ,D D、E E分分别是是CC1CC1和和A1BA1B的中点,的中点,AC=AA1=2AC=AA1=2 (1) (1)求求线段段DEDE的的长B1B1B BA AD DA1A1E EC CC1C1F解:取解:取ABAB的中点的中点F F,连结,连结EFEF,CFCF,EF/AA1/CC1EF/AA1/CC1DD是中点,是中点,EF CDEF CDDE=CFDE=CF在在ABCABC中,中,CFCFDEDE前往例题讲解例题讲解2 2、如、如图在直三棱柱在直三棱柱ABC-A1B1C1ABC-A1B1C1中,底面中,底面ABCABC是等腰是等腰RtRt, C=900 C=900 ,D D、E E分分别是是CC1CC1和和A1BA1B的中点,的中点,AC=AA1=2AC=AA1=2(2)(2)求二面角求二面角A-BD-CA-BD-C的大小的大小( (反三角表示反三角表示) )MB1B1B BA AD DA1A1E EC CC1C1解:解: ABC-A1B1C1 ABC-A1B1C1是直棱柱,是直棱柱,ACBCACBC,ACAC侧面面BB1C1CBB1C1C,作作CMBDCMBD于于M M,连结AMAM,那么那么AMCAMC就是所求二面角的平面角;就是所求二面角的平面角;在在ACMACM中,中,ACAC2 2CMCMtanAMC=AC/CM=tanAMC=AC/CM=即所求为即所求为ACCMACCM,前往例题讲解例题讲解3 3、如、如图在直三棱柱在直三棱柱ABC-A1B1C1ABC-A1B1C1中,底面中,底面ABCABC是等腰是等腰RtRt,C=900 C=900 ,D D、E E分分别是是CC1CC1和和A1BA1B的中点,的中点,AA1AA12 2,假,假设点点E E在平面在平面ABDABD上的射影是上的射影是ABDABD的重心的重心G.G. (1) (1)求求A1BA1B与平面与平面ABDABD所成的角所成的角( (用反三角表示用反三角表示) );B1B1B BA AD DA1A1E EC CC1C1GFM解:解:连结BGBG,由知,由知EBGEBG就是所求的角,就是所求的角, A1BA1B与平面与平面ABDABD所成的角所成的角为前往例题讲解例题讲解3 3、如、如图在直三棱柱在直三棱柱ABC-A1B1C1ABC-A1B1C1中,底面中,底面ABCABC是等腰是等腰RtRt,C=900 C=900 ,D D、E E分分别是是CC1CC1和和A1BA1B的中点,的中点,AA1AA12 2,假,假设点点E E在平面在平面ABDABD上的射影是上的射影是ABDABD的重心的重心G.G. (2) (2)求点求点A1A1到平面到平面AEDAED的的间隔。隔。B1B1B BA AD DA1A1E EC CC1C1方法方法A A:作垂:作垂线法法方法方法B B:等体:等体积法法前往3 3、如、如图在直三棱柱在直三棱柱ABC-A1B1C1ABC-A1B1C1中,底面中,底面ABCABC是等腰是等腰RtRt,C=900 C=900 ,D D、E E分分别是是CC1CC1和和A1BA1B的中点,的中点,AA1AA12 2,假,假设点点E E在平面在平面ABDABD上的射影是上的射影是ABDABD的重心的重心G.G. (2) (2)求点求点A1A1到平面到平面AEDAED的的间隔。隔。B1B1B BA AD DA1A1E EC CC1C1FMK解解A A:由上:由上题解知,解知,DEDE平面平面AA1B1BAA1B1B平面平面ADEADE平面平面AA1B1BAA1B1B于于AEAE在在A1AB1A1AB1中,中,A1KA1K方法方法A A:作垂线法:作垂线法前往3 3、如、如图在直三棱柱在直三棱柱ABC-A1B1C1ABC-A1B1C1中,底面中,底面ABCABC是等腰是等腰RtRt,C=900 C=900 ,D D、E E分分别是是CC1CC1和和A1BA1B的中点,的中点,AA1AA12 2,假,假设点点E E在平面在平面ABDABD上的射影是上的射影是ABDABD的重心的重心G.G. (2) (2)求点求点A1A1到平面到平面AEDAED的的间隔。隔。B1B1B BA AD DA1A1E EC CC1C1解解B B:方法方法B B:等体积法:等体积法方法方法C C:对象象转换法法前往小结:小结:1 1、联想概念及其性想概念及其性质;2 2、分解、分解难点,掌握各点,掌握各类根本作根本作图;3 3、强调作作证求求过程;程;4 4、空、空间问题平面化,尤三角形内平面化,尤三角形内 的的计算。算。前往面积问题体积问题根底根底题例例题C1.设设棱棱锥锥的底面面的底面面积为积为8cm2,那么,那么这这个棱个棱锥锥的中截面的中截面(过过棱棱锥锥的的中中点点且且平平行行于于底底面面的的截截面面)的的面面积积是是( ) (A)4cm2 (B) cm2 (C)2cm2 (D) cm22. 一一个个锥体体被被平平行行于于底底面面的的平平面面所所截截,假假设截截面面面面积是是底底面面面面积的的四四分分之之一一,那那么么锥体体被被截截面面截截得得的的一一个个小小锥与原棱与原棱锥体体积之比之比为 ( ) (A)1 : 4 (B) 1 : 3 (C) 1 : 8 (D) 1 : 7 C前往A3.设设长长方方体体三三条条棱棱长长分分别别为为a,b,c,假假设设长长方方体体一一切切棱棱的的长长度之和度之和为为24,一条,一条对对角角线长线长度度为为5 ,体,体积为积为2,那么,那么 等于等于 ( ) (A) (B) (C) (D)根底根底题例例题前往C4.斜三棱柱的一个斜三棱柱的一个侧侧面的面面的面积为积为S,另一条,另一条侧侧棱到棱到这这个个侧侧面面的的间间隔隔是是a,那那么么这这个个三三棱棱柱柱的的体体积积是是 ( ) (A) (B) (C) (D)根底根底题例例题5.在在侧棱棱长为23,每每个个侧面面的的顶角角均均为40的的正正三三棱棱锥P-ABC中中,过A作作截截面面分分别交交PB、PC于于E、F,那那么么AEF的最小周的最小周长是是 ( ) (A) 6 (B) (C) 36 (D) A前往例例设P是棱是棱长相等的四面体内恣意一点,相等的四面体内恣意一点,那么那么P到各个面的到各个面的间隔之和是一个定隔之和是一个定值,这个定个定值等于等于 。 A四面体的棱四面体的棱长 B四面体的斜高四面体的斜高 C四面体的高四面体的高 D四面体两四面体两对棱棱间的的间隔隔提示:用体提示:用体积法求解法求解前往解:如解:如图正四面体正四面体ABCD中,中,过点点A作四面体作四面体的高的高AO,那么由点,那么由点P分分别衔接接PA、PB、PC、PD,得到四个小四面体,得到四个小四面体, 假假设点点P到四个外表的到四个外表的间隔分隔分别为h1、h2、h3、h4,那么四面体被分成的四个小四面体,那么四面体被分成的四个小四面体,它它们的体的体积和恰好是四面体和恰好是四面体ABCD的体的体积,前往 VABCD=VPBCD+VPABC+VPABD+VPACD, h1+h2+h3+h4=AO. 选C.前往例假设正四棱柱的底面积为例假设正四棱柱的底面积为P,过相对两,过相对两侧棱的截面面积是侧棱的截面面积是Q,那么该四棱柱的体积,那么该四棱柱的体积是是 。 A B C D前往解:如图,设四棱柱底面边长AB=a,高AA1=b,那么P=a2,过两侧棱AA1、CC1的截面面积Q= ab, 四棱柱的体四棱柱的体积选选A前往6.假假设一一个个斜斜棱棱柱柱A1B1C1ABC的的底底面面是是等等腰腰ABC,它它的的三三边边长分分别是是AB=AC=10cm,BC=12cm,棱棱柱柱的的顶点点A1与与A、B、C三三点点等等距距,且且侧棱棱AA1=13cm,求求此此棱棱柱柱的的全面全面积.B A1 A C B1 C1 解:自解:自B引引BDAA1于于D,衔接接CD,DAA1=A1B=A1C,底面底面ABC为等腰等腰,故故顶点点A1在底面在底面ABC上的射影上的射影O在底在底边BC的高的高AE上,上,OE由三垂由三垂线定理知,定理知,BCAA1, 即即侧面面B1BCC1为矩形,矩形,由由AA1BC,AA1BD,得得AA1平面平面BDC,AA1CD,在在A1AB中,引中,引A1FAB于于F,F在在RtA1FA中,由中,由A1A=13,AF=5,A1F=12,得得那么那么BD=ABsinA1AB=10S柱柱侧=(BD+DC+BC)A1A=396,又在又在ABC中,中,AEBC,AB=10,BE=6,得得AE=8,SABC=8,S柱全柱全=396+248=492(cm) 2前往例例: :如如图知正三棱知正三棱锥S ABCS ABC中中,E,E、F F分分别是是SBSB、SC SC 的中点,平面的中点,平面AEFAEF平面平面SCB.SCB.求求证:三棱:三棱锥SABCSABC侧面面 积与底面与底面积的比。的比。解:作正棱锥的高SO,连结AO并延伸交BC于D, 连结SD交EF于G,连结AG.SO平面ABC,O是ABC中心D是BC的中点.又EF是SBC的中位线G是SD的中点根据对称性,AE=AFAGEF平面AEF平面SCBAG平面SBC,AGSD,ASD是等腰三角形,SA=DAABDCSFEGO前往设正三棱锥SABC的底面边长为 ,那么AD= ,SA=SB=于是: S侧SABC3 SD BC AD BC3SD=AD=ABDCSFEGO前往ABCSD例例1 1、知三棱锥的两个侧面都是边长为、知三棱锥的两个侧面都是边长为 的等的等边三角形,另一个侧面是等腰直角三角形。求此边三角形,另一个侧面是等腰直角三角形。求此三棱锥的体积。三棱锥的体积。法一:取法一:取ABAB中点中点D D,衔接接SDSD,CDCD。易得易得ABCABC为等腰直角三角形,等腰直角三角形,ACB=90oACB=90o。那么有。那么有SDABSDAB,CDABCDAB。又。又SA=SB=SCSA=SB=SC,SS在底面的射影在底面的射影为底面的外心,底面的外心,即点即点D D,SDSD平面平面ABCABC。由由VS-ABC= SABCSDVS-ABC= SABCSD得三棱得三棱锥体体积。前往例、知三棱锥的两个侧面都是边长为例、知三棱锥的两个侧面都是边长为 的等边三角的等边三角形,另一个侧面是等腰直角三角形。求此三棱锥的体积。形,另一个侧面是等腰直角三角形。求此三棱锥的体积。ABCSEF留意:分割法求体留意:分割法求体积。解法二解法二提示:设三棱锥提示:设三棱锥S-ABCS-ABC,侧面,侧面SACSAC、SBCSBC为等边三角形,边长为为等边三角形,边长为 ,SASA SBSB。取。取SASA中点中点E E,ABAB中点中点F F,衔接,衔接AEAE、BEBE、EFEF。可证得:。可证得:SC SC 平面平面ABEABE。利用:利用:VS-ABC=VS-ABE+VC-ABEVS-ABC=VS-ABE+VC-ABE得三棱锥体积。得三棱锥体积。KEY: 前往例、在棱长为例、在棱长为a a的正方体的正方体ABCD-A1B1C1D1ABCD-A1B1C1D1中,中,求求D1D1到截面到截面C1BDC1BD的间隔。的间隔。ABCDA1B1C1D1提示:利用提示:利用 = 求解。求解。留意:等体留意:等体积法求点面法求点面间隔。隔。KEY:前往例:如例:如图,在,在长方体方体ABCDABCDA1B1C1D1A1B1C1D1中,中,AD=AA1=1AD=AA1=1,AB=2AB=2,点,点E E在棱在棱ABAB上挪上挪动证明:明:D1EA1DD1EA1D;当当E E为ABAB的中点的中点时, ,求点求点E E到面到面ACD1ACD1的的间隔;隔;AEAE等于何等于何值时,二面角,二面角D1D1ECECD D的大小的大小为AA1BDECB1C1D1等体等体积法求点面法求点面间隔隔前往PBCDEA例:知四棱例:知四棱锥PABCD PABCD ,PBADPBAD,侧面面PADPAD为边长等于等于2 2的正三角形,底面的正三角形,底面ABCDABCD为菱形,菱形,侧面面PADPAD与底面与底面ABCDABCD所成的二面角所成的二面角为120120。求点求点P P到平面到平面ABCDABCD的的间隔;隔;求面求面APBAPB与面与面CPBCPB所成二面角的大小。所成二面角的大小。等体等体积法求点面法求点面间隔隔经过以上的解答以上的解答, ,我我们不不难看出等体看出等体积法在法在处置点到置点到面的面的间隔和体隔和体积时非常有效非常有效, ,因此我因此我们在平常的学在平常的学习中中应该掌握掌握. .利用等体利用等体积法我法我们可以从可以从侧面迂回地面迂回地处理一些从正面理一些从正面较难下手的下手的问题这是数学中的一是数学中的一种重要思想方法种重要思想方法. .在利用等体在利用等体积法法时我我们应该在原在原图形中形中寻觅到一个到一个较容易容易计算出面算出面积及其高的面来。及其高的面来。前往C3.设设棱棱锥锥的底面面的底面面积为积为8cm2,那么,那么这这个棱个棱锥锥的中截面的中截面(过过棱棱锥锥的的中中点点且且平平行行于于底底面面的的截截面面)的的面面积积是是( ) (A)4cm2 (B) cm2 (C)2cm2 (D) cm2前往4.假假设一一个个锥体体被被平平行行于于底底面面的的平平面面所所截截,假假设截截面面面面积是是底底面面面面积的的四四分分之之一一,那那么么锥体体被被截截面面截截得得的的一一个个小小锥与原棱与原棱锥体体积之比之比为( ) (A)1 : 4 (B) 1 : 3 (C) 1 : 8 (D) 1 : 7 C前往A5.设设长长方方体体三三条条棱棱长长分分别别为为a,b,c,假假设设长长方方体体一一切切棱棱的的长长度之和度之和为为24,一条,一条对对角角线长线长度度为为5 ,体,体积为积为2,那么,那么 等于等于( ) (A) (B) (C) (D)前往C6.斜三棱柱的一个斜三棱柱的一个侧侧面的面面的面积为积为S,另一条,另一条侧侧棱到棱到这这个个侧侧面的面的间间隔是隔是a,那么,那么这这个三棱柱的体个三棱柱的体积积是是( ) (A) (B) (C) (D)前往A7.在在侧棱棱长为23,每每个个侧面面的的顶角角均均为40的的正正三三棱棱锥P-ABC中中,过A作作截截面面分分别交交PB、PC于于E、F,那那么么AEF的最小周的最小周长是是( ) (A) 6 (B) (C) 36 (D) 前往8. 如如图,在多面体,在多面体ABCDE中,中,AE面面ABC,BDAE,且,且AC=AB=BC=BD=2,AE=1,F为CD中点中点(1)求求证:EF面面BCD;(2)求多面体求多面体ABCDE的体的体积;(3)求面求面CDE与面与面ABDE所成的二面角的余弦所成的二面角的余弦值.【解解题题回回想想】对对于于不不规规那那么么几几何何体体一一定定要要能能识识别别其其本本质质,此此题题的的多多面面体体实实践践上是倒着的四棱上是倒着的四棱锥锥. .前往9.在在三三棱棱锥P-ABC中中,PA、PB、PC两两两两成成60角角,PA=a,PB=b,PC=c,求三棱,求三棱锥P-ABC的体的体积. 【解解题题回回想想】(1)把把A、B、C中中的的任任一一个个点点作作为为顶顶点点(其其他他三三点点构构成成的的三三角角形形作作为为底底面面)是是解解题题的的关关键键,这这阐阐明明改改动动几几何何体体的的放放置置方方式式或或改改动动对对几几何何体体的的察察看看角角度在解度在解题题中是非常重要的中是非常重要的.(2)当当a=b=c时时,得到正四面体的体,得到正四面体的体积积是是?.(3)假假设设在在PA、PB、PC上上各各任任取取一一点点M、N、R,设设PM=m,PN=n,PR=r,那那么么容容易易证证明明 ,这这一一结结论论与与PA、PB、PC成多大的角无关成多大的角无关.前往10.假假设一一个个斜斜棱棱柱柱A1B1C1ABC的的底底面面是是等等腰腰ABC, 它它 的的 三三 边 边 长 分分 别 是是 AB=AC=10cm,BC=12cm,棱棱柱柱的的顶点点A1与与A、B、C三三点点等等距距,且且侧棱棱AA1=13cm,求此棱柱的全面,求此棱柱的全面积.【解解题回回想想】求求斜斜棱棱柱柱全全面面积的的根根本本方方法法是是求求出出各各个个侧面面的的面面积与与底底面面积.此此题求求侧面面积时也也可可以以用用直直截截面面BCD的周的周长去乘去乘AA1而得到而得到.ABCA1B1C1E前往误解分析解分析1.1.求求斜斜棱棱柱柱的的全全面面积,除除直直截截面面周周长乘乘侧棱棱长这个个公公式式外外,大大多多采采用用逐逐一一求求出出各各外外表表面面积,然然后后作作和和的的方方法法,因因此此不不要要盲盲目目套套什什么么公式,或在相加公式,或在相加时,漏了上、下底面,漏了上、下底面积2.2.求求三三棱棱锥的的体体积非非常常灵灵敏敏,有有直直接接法法、割割补法法、颠倒倒顶点点法法等等,不不论用用何何种种方方法法,一一定要看清字母位置,更不能漏乘定要看清字母位置,更不能漏乘1/3.1/3.前往与球的多面体问题例一个凸多面体的棱数例一个凸多面体的棱数为30,面数,面数为12,那么它的各面多那么它的各面多边形的内角形的内角总合是合是 A5400 B6480 C7200 D7920提示:运用提示:运用“欧拉定理欧拉定理 E+2=V+F。前往解:根据欧拉定理解:根据欧拉定理 V=(E+2)F=3212=20.设该多面体的多面体的12个面的个面的边数分数分别为E1,E2,E12,那么共有棱数那么共有棱数30= ( E1+E2+E12), E1+E2+E12=60,12个面中每个面的内角个面中每个面的内角为i=1,2,12, 内角内角总合合为 =6480, 选B.前往知知凸凸多多面面体体每每个个面面都都是是五五边边形形,每每个个顶顶点点都都有有三三条条棱棱,试试求求该该多多面面体体的的面面数数、顶顶点点数数和和棱数棱数.【解解题题回回想想】用用欧欧拉拉公公式式V+F-E=2解解题题时时,要要擅擅长长发发现棱数现棱数E与面数与面数F、顶点数、顶点数V的关系,普通有的关系,普通有和和前往A1.一一个个四四面面体体的的一一切切棱棱长都都为2,四四个个顶点点在在同同一一球球面面上,那么此球的外表上,那么此球的外表积为 ( ) (A) (B) (C) (D)根底根底题例例题2.地球外表上从地球外表上从A地地(北北纬45,东经120)到到B地地(北北纬45,东经30)的最短的最短间隔隔为(地球半径地球半径为R) ( )(A)R (B) (C) (D)C3.在北在北纬45o的圈上有甲、乙、丙三地,甲乙、乙丙之的圈上有甲、乙、丙三地,甲乙、乙丙之间的的经度差都是度差都是90o,那么甲丙两地的球面,那么甲丙两地的球面间隔是甲乙两地隔是甲乙两地球球面面间隔的隔的 _倍倍 前往根底根底题例例题C4.球的外表球的外表积膨膨胀为原来的原来的 2 倍,膨倍,膨胀后的体后的体积为原来的原来的 A. 2倍倍 B.2倍倍 C.22倍倍 D.4倍倍5.棱棱长为2的正四面体的体的正四面体的体积为_6.设P、A、B、C是球是球O面上的四点,且面上的四点,且PA、PB、PC两两两两相互垂直,假相互垂直,假设PA=PB=PC=a, 那么球心那么球心O到截面到截面ABC的的间隔隔是是_前往才干才干 思想思想 方法方法7.求正八面体每相邻两个面所成二面角的大小。求正八面体每相邻两个面所成二面角的大小。ABCFDE解:如解:如图,设棱棱长为 a,AE中点中点为F, 衔接接BF、DF, ABE,ADE是正三角形,是正三角形, BFAE,DFAE, BFD是二面角是二面角B-AE-D的平面角,的平面角, BDF中,中,BF=DE= BD= 所求二面角所求二面角为- arccos 前往三棱锥三棱锥A-BCD的两条棱的两条棱AB=CD=6,其他各棱长均为其他各棱长均为5,求,求 三棱锥的内切球半径三棱锥的内切球半径.EDCBA解:取解:取CD的中点的中点E,衔接接AE,BE,由由CDAE,CDBE,得得CD平面平面ABE又又AD=5,DE=3,得,得AE=BE=4,故故ABE的面的面积为37于是,于是,VA-BCD=VC-ABE+VD-ABE显然,三棱然,三棱锥的三个的三个侧面全等,各面全等,各侧面的面面的面积为12,设三棱三棱锥的内切球半径的内切球半径为 r,那么,那么VA-BCD= (SABC+SBCD+SCDA+SDAB)r= 48r =16r 由由16r=67 得内切球的半径得内切球的半径为 前往【解【解题回想】回想】正正 如如 三三 角角 形形 的的 内内 切切 圆 经 常常 与与 面面 积 发 生生 关关系一系一样,多面体的内切球的半径也常与体,多面体的内切球的半径也常与体积发生生联络.才干才干 思想思想 方法方法前往才干才干 思想思想 方法方法9.在球内有相距在球内有相距14cm 的两个平行截面,它的两个平行截面,它们的面的面积分分别是是 64cm2 和和 36cm2,求球的外表,求球的外表积。.解:解:设球半径球半径为R,1当截面在球心同当截面在球心同侧,如,如图11那么有那么有R2-36-R2-64=14 而此方程无解,故截面在球心的同而此方程无解,故截面在球心的同侧不能不能够。2当截面在球心异当截面在球心异侧,如,如图22那么有那么有R2-36 +R2-64=14解得解得 R=10 S球面球面=4R2=400(cm)2前往例:共端点例:共端点M的三条的三条线段段MA、MB、MC两两两垂直,两垂直,过M、A、B、C刚好可作一个半径好可作一个半径为2的球,那么的球,那么MA、MB、MC的平方和的平方和为 解:以解:以MA、MB、MC为棱作棱作长方体,那么方体,那么这个个长方体的八个方体的八个顶点都在球上,且点都在球上,且长方体的方体的对角角线恰好是球的直径,所以球的直径恰好是球的直径,所以球的直径d=4,而而MA2+MB2+MC2=d2=16.前往延伸拓展过过半半径径为为R的的球球面面上上一一点点作作三三条条两两两两垂垂直直的的弦弦MA、MB、MC.(1)求证:求证:MA2+MB2+MC2为定值;为定值;(2)求三棱锥求三棱锥M-ABC的体积的最大值的体积的最大值.【解解题回回想想】(1)MA、MB、MC两两两两垂垂直直.根根据据球球的的对称称性性,采采用用补形形的的方方法法,可可以以把把它它补成成一一个个球球的的内内接接长方方体体.长方方体体的的对角角线的的平平方方就就是是球球的的直直径径的的平平方方,即即MA2+MB2+MC2=4R2.在在做做选择题、填填充充题时就就可可直接用直接用这个个结论.(2)在在球球中中的的线段段计算算问题,常常转化化为小小圆半半径径,大大圆半径及球心到截面半径及球心到截面间隔来隔来处理理. 前往前往前往误解分析解分析1.1.在涉及球内接正方体或在涉及球内接正方体或长方体的方体的标题中,中,作出的截面普作出的截面普经过多面体的多面体的对角角线,且,且对角角线长为球的直径球的直径假假设过对棱中点作横截面,棱中点作横截面,将会出将会出错. .2.2.球球面面上上两两点点间间隔隔不不是是直直线间隔隔,也也不不是是纬度度圈圈上上的的劣劣弧弧长,而而是是指指过这两两点点的的球球大大圆上上 的劣弧的劣弧长,不能,不能错啊啊! !前往例:如下例:如下图,在,在纬度度为的北的北纬纬线上有一点上有一点A,其中,其中是是AOO的三内角的等差中的三内角的等差中项,而,而t是是 与与 的等比中的等比中项,当地球,当地球自自转t小小时后,求点后,求点A转动前后的球面前后的球面间隔隔前往解:由解:由题意得意得 =60 , , t=6,设点点A转动后后为点点B,由于地球,由于地球转一圈需一圈需24小小时,因此,因此6小小时转了了圆周周长的的 ,所以所以AOB=90, OAO=30,所以所以AOB=90, OAO=30,所以所以AO=Rsin30= R=BO, AB= R, 前往由余弦定理得:由余弦定理得:cosAOB= AOB=arccos ,A点点转动前后的球面前后的球面间隔隔为Rarccos .前往A1.一一个个四四面面体体的的一一切切棱棱长长都都为为2,四四个个顶顶点点在在同同一一球球面面上,那么此球的外表积为上,那么此球的外表积为( ) (A) (B) (C) (D)A2.知知一一个个简单多多面面体体的的各各个个顶点点处都都有有三三条条棱棱,那那么么顶点数点数V与面数与面数F满足的关系式是足的关系式是( ) (A)2F+V=4 (B)2F-V=4 (C)2F+V=2 (D)2F-V=2前往A3.一一个个凸凸多多面面体体的的顶点点数数为20,棱棱数数为30.那那么么它它的的各各面多面多边形的内角形的内角总和和为( ) (A)2160 (B)5400 (C)6480 (D)7200A4.将将棱棱长为3的的正正四四面面体体的的各各棱棱长三三等等分分,经过接接近近顶点点的的各各分分点点,将将原原正正四四面面体体各各顶点点均均截截去去一一个个棱棱长为1的小正四面体,剩下的多面体的棱数的小正四面体,剩下的多面体的棱数为( ) (A)16 (B)17 (C)18 (D)19前往A5.地球外表上从地球外表上从A地地(北北纬45,东经120)到到B地地(北北纬45,东经30)的最短的最短间隔隔为(地球半径地球半径为R)( )(A)R (B)(C) (D)前往翻折问题生活问题 如图,以等腰直角三角形斜边BC上的高AD为折痕,使 ABD和 ACD折成相垂直的两个面。求证:1BDCD;2 BAC=60.ABCDABCD前往例例:知知:E、F是是正正方方形形ABCD的的边BC和和CD的的中中 点点 , 分分 别 沿沿 AE、 EF、 AF将将 ABE、 ECF、AFD折折起起,使使B、C、D三三点点重重合合于于P点点,如下如下图。1求求证:APEF;2求二面角求二面角A-EF-P的大小。的大小。 前往解:1APPF,AP PE, PEPE=P AP平面PEF 又EF 平面PEF AP EF.前往2取取EF的中点的中点H,连结PH、AH,PE=PF,AE=AFAHEF,PHEFAHP是二面角是二面角A-EF-P的平面角。的平面角。由由(1)知知AP平面平面PEF,而,而PH平面平面PEFAPPH,即,即APH是是Rt.cosAHP=,AHP=arcos二面角二面角A-EF-P的大小的大小为arcos。前往 例:在矩形ABCD中,AB=3,BC=4,沿对角线BD对折成二面角A-BD-C,使A在平面BCD上的射影在BC上。 1求异面直线AB与CD所成的角; 2 求AB和CD间的间隔。前往 例3:知RtABC中,AB=3,BC=4,E是斜边AC边上的一点,沿BE将ABE折起,使二面角A-BE-C是直二面角,当AC最短时,求ABE的大小。前往练习练习 1 1、长方体、长方体ABCD-A1B1C1D1ABCD-A1B1C1D1中,中,AB=3AB=3,BC=2BC=2,AA1=1AA1=1,一蚂蚁从点,一蚂蚁从点A A沿其外表沿其外表爬爬到到C1C1点的最短路程为点的最短路程为 A A、 B B、 C C、 D D、 前往2、如如图图代代表表未未折折叠叠正正方方体体的的展展开开图图,将将其其折折叠叠起起来来,变成正方体后图形是变成正方体后图形是前往5.5.如图是正方体的平面展开图,在这个正方体中如图是正方体的平面展开图,在这个正方体中BM与与ED平行;平行;CN与与BE是异面直是异面直线;CN与与BM成成60的角;的角;DM与与BN垂直。垂直。以上四个命题中,正确以上四个命题中,正确命题的序号是命题的序号是AEDCBFNMAEDCBFNM前往复习小结复习小结1、解折叠问题首先是准确地画出原、解折叠问题首先是准确地画出原来的平面图形及折叠后的空间图形来的平面图形及折叠后的空间图形,对照两图形中对应元素的位置、大对照两图形中对应元素的位置、大小、外形小、外形,确定不变元素,不变量是确定不变元素,不变量是解题的根底解题的根底,折叠所成的二面角往往折叠所成的二面角往往是解题的关键。是解题的关键。前往2、求、求侧面上两点面上两点间的最短的最短间隔隔,普通都是将空普通都是将空间图形沿某形沿某一条棱或母一条棱或母线剪开剪开铺平,化平,化为求两点决求两点决议的的线段段长,从而从而化化“曲曲为“直,化直,化“折折为“平。展开是空平。展开是空间问题平面平面化的一种常用方法。化的一种常用方法。前往一一个个立立方方体体的的六六个个面面上上分分别标有有字字母母A A、B B、C C、D D、F F,以以下下图是是此此立立方方体体的的两两种种不不同同放放 置置 , 那那 么么 与与 D D面面 相相 对 的的 面面 上上 的的 字字 母母 是是 ( ( ) )B前往如如图,以以长方方体体ABCD-A1B1C1D1ABCD-A1B1C1D1的的顶点点为顶点点且且四四个个面面都都是是直直角角三三角角形形的的四四面面体是体是_( (注注:只只写写出出其其中中的的一一个个,并并在在图中中画画出相出相应的四面体的四面体) ) 前往一一间民民房房的的屋屋顶有有如如下下图三三种种不不同同的的盖盖法法:单向向倾斜斜;双双向向倾斜斜;四四向向倾斜斜. .记三三种种盖盖法法屋屋顶面面积分分别为P1P1、P2P2、P3.P3.假假设屋屋顶斜斜面与程度面所成的角都是面与程度面所成的角都是,那么,那么 ( ) ( )(A)P3(A)P3P2P2P1P1(B)P3(B)P3P2=P1P2=P1(C)P3=P2(C)P3=P2P1P1(D)P3=P2=P1(D)P3=P2=P1 D前往知知甲甲烷CH4CH4的的分分子子构构造造是是:中中心心一一个个碳碳原原子子,外外围有有4 4个个氢原原子子( (这4 4个个氢原原子子构构成成一一个个正正四四面面体体的的四四个个顶点点).).设中中心心碳碳原原子子到到外外围4 4个个氢原原子子连成成的的四四条条线段段两两两两组成成的的角角为,那那么么coscos等于等于 ( ) ( )(A)-1/3 (B)1/3(A)-1/3 (B)1/3(C)-1/2 (D)1/2(C)-1/2 (D)1/2A前往在在直直角角坐坐标系系xoyxoy中中,点点A A、B B、C C、D D的的坐坐标分分别为(5(5,0)0)、(-3(-3,0)0)、(0(0,-4)-4)、(-4(-4,-3)-3),将坐将坐标平面沿平面沿y y轴折成直二面角折成直二面角. .(1)(1)求求ADAD、BCBC所成的角;所成的角;(2)BC(2)BC、ODOD相交于相交于E E,作,作EFADEFAD于于F F,求求证:EFEF是是ADAD、BCBC的公垂的公垂线,并求出公垂,并求出公垂线段段EFEF的的长;(3)(3)求四面体求四面体C-AODC-AOD的体的体积. .【解【解题回想】回想】这是一道与解几是一道与解几结合的翻折合的翻折题,画好折后,画好折后图将原平面将原平面图复原成四棱复原成四棱锥,进一步用三垂一步用三垂线定定理理证明明ADBC.ADBC.前往1 1给出两出两块一一样的正三角形的正三角形纸片如片如图1 1,图2 2,要求用其中一要求用其中一块剪拼成一个正三棱剪拼成一个正三棱锥模型,另一模型,另一块剪剪拼成一个正三棱柱模型,使它拼成一个正三棱柱模型,使它们的全面的全面积都与原三角都与原三角形的面形的面积相等,相等,请设计一种剪拼方法,分一种剪拼方法,分别用虚用虚线标示在示在图1 1、图2 2中,并作中,并作简要要阐明;明;2 2试比比较他剪拼的正三棱他剪拼的正三棱锥与正三棱柱的体与正三棱柱的体积的的大小;大小;3 3本小本小题为附加附加题 假假设给出的是一出的是一块恣意三角形的恣意三角形的纸片如片如图3 3,要求剪拼成一个直三棱柱模型,使它要求剪拼成一个直三棱柱模型,使它们的全面的全面积与与给出的三角形的面出的三角形的面积相等,相等,请设计一种剪拼方法,用虚一种剪拼方法,用虚线标示在示在图3 3中,并作中,并作简要要阐明明. .图1图2前往【解解题回回想想】此此题是是2019年年高高考考题,是是一一道道集集开开放放、探探求求、动手手于于一一体体的的优秀秀考考题,正正三三角角形形剪剪拼拼正正三三棱棱柱柱除除参参考考答答案案的的那那种种剪剪法法外外,还可可以以用用如如图4的的剪剪法法,当当然然参参考考答答案案的的剪剪法法是是其其本本质解解,由由于于它它为3的的解解答提供了答提供了协助助.图1图2图3图4前往5.如如图(甲甲),从从三三棱棱锥P-ABC的的顶点点P沿沿着着三三条条侧棱棱PA、PB、PC剪剪开开成成平平面面图形形,得得到到P1P2P3(如如图(乙乙),且,且P1P2=P2P3.(1)在三棱在三棱锥P-ABC中,求中,求证:PABC.(2)假假设P1P2=26,P1P3=20,求三棱,求三棱锥P-ABC的体的体积.前往综合问题球面上点的问题球面上点的问题ABCOpABCOpM前往练习题练习题BC前往
网站客服QQ:2055934822
金锄头文库版权所有
经营许可证:蜀ICP备13022795号 | 川公网安备 51140202000112号

