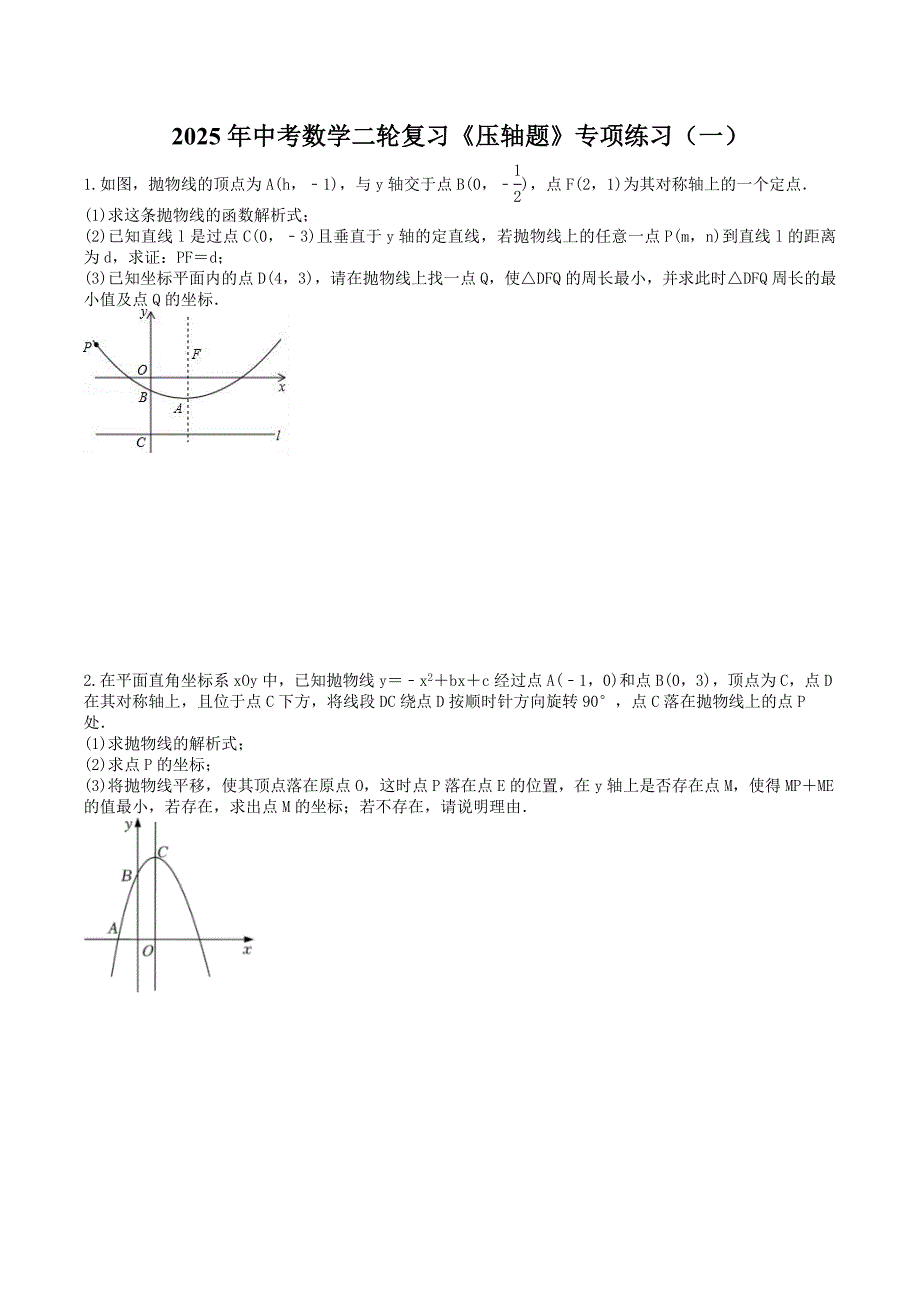
2025年中考数学二轮复习压轴题专项练习（一）如图，抛物线的顶点为A(h，1)，与y轴交于点B(0，)，点F(2，1)为其对称轴上的一个定点(1)求这条抛物线的函数解析式；(2)已知直线l是过点C(0，3)且垂直于y轴的定直线，若抛物线上的任意一点P(m，n)到直线l的距离为d，求证：PFd；(3)已知坐标平面内的点D(4，3)，请在抛物线上找一点Q，使DFQ的周长最小，并求此时DFQ周长的最小值及点Q的坐标在平面直角坐标系xOy中，已知抛物线yx2bxc经过点A(1，0)和点B(0，3)，顶点为C，点D在其对称轴上，且位于点C下方，将线段DC绕点D按顺时针方向旋转90，点C落在抛物线上的点P处(1)求抛物线的解析式；(2)求点P的坐标；(3)将抛物线平移，使其顶点落在原点O，这时点P落在点E的位置，在y轴上是否存在点M，使得MPME的值最小，若存在，求出点M的坐标；若不存在，请说明理由如图，已知抛物线y=x2+bx+c与x轴交于点A(1，0)、C，与y轴交于点B(0，3)，抛物线的顶点为P(1)求抛物线的解析式；(2)若抛物线向下平移k个单位后经过点(5，6)求k的值及平移后抛物线所对应函数的最小值；设平移后抛物线与y轴交于点D，顶点为Q，点M是平移后的抛物线上的一个动点，请探究：当点M在何处时，MBD的面积是MPQ面积的2倍？求出此时点M的坐标如图，抛物线yx2bxc过点B(3，0)，C(0，3)，D为抛物线的顶点(1)求抛物线的解析式以及顶点坐标；(2)连接BC，CD，DB，求CBD的正切值；(3)点C关于抛物线yx2bxc对称轴的对称点为E点，连接BE，直线BE与对称轴交于点M，在(2)的条件下，点P是抛物线对称轴上的一点，是否存在点P使CDB和BMP相似，若存在，求点P坐标，若不存在，请说明理由如图，抛物线yx2bxc的顶点D坐标为(1，4)，且与x轴相交于A，B两点(点A在点B的左侧，与y轴相交于点C，点E在x轴上方且在对称轴左侧的抛物线上运动，点F在抛物线上并且和点E关于抛物线的对称轴对称，作矩形EFGH，其中点G，H都在x轴上(1)求抛物线解析式；(2)设点F横坐标为m，用含有m的代数式表示点E的横坐标为 (直接填空)；当矩形EFGH为正方形时，求点G的坐标；连接AD，当EG与AD垂直时，求点G的坐标；(3)过顶点D作DMx轴于点M，过点F作FPAD于点P，直接写出DFP与DAM相似时，点F的坐标如图，在平面直角坐标系中，矩形OABC的顶点A，C分别在x轴，y轴的正半轴上，且OA4，OC3，若抛物线经过O，A两点，且顶点在BC边上，对称轴交AC于点D，动点P在抛物线对称轴上，动点Q在抛物线上.(1)求抛物线的解析式；(2)当POPC的值最小时，求点P的坐标；(3)是否存在以A，C，P，Q为顶点的四边形是平行四边形？若存在，请直接写出P，Q的坐标；若不存在，请说明理由.已知二次函数yax2bxc(a0)与x轴交于A(x1，0)，B(x2，0)两点，且(x10x2)，交y轴于点C，顶点为D(1)a1，b2，c4，求该二次函数的对称轴方程及顶点坐标；定义：若点P在某函数图象上，且点P的横纵坐标互为相反数，则称点P为这个函数的“零和点”，求证：此二次函数有两个不同的“零和点”；(2)如图，过D、C两点的直线交x轴于点E，满足ACECBE，求ac的值抛物线y=ax2+bx+2与x轴交于点A(3，0)、B(1，0)，与y轴交于点C.(1)求抛物线的解析式(2)在抛物线对称轴上找一点M，使MBC的周长最小，并求出点M的坐标和MBC的周长(3)若点P是x轴上的一个动点，过点P作PQBC交抛物线与点Q，在抛物线上是否存在点Q，使B、C、P、Q为顶点的四边形为平行四边形？若存在请求出点Q的坐标，若不存在请说明理由.已知抛物线L1：yax2bxc(a0)与x轴交于点A(1，0)，点B(3，0)，与y轴交于点C(0，3)(1)求抛物线L的表达式；(2)若点P是直线yx1上的一个动点，将抛物线L进行平移得到抛物线L，点B的对应点为点Q，是否存在以A、B、P、Q四个点为顶点的四边形是菱形？若存在，求出抛物线的平移方式；若不存在，请说明理由抛物线yax2bxc与直线y有唯一的公共点A，与直线y交于点B，C(C在B的右侧)，且ABC是等腰直角三角形过C作x轴的垂线，垂足为D(3，0)(1)求抛物线的解析式；(2)直线y2x与抛物线的交点为P，Q，且P在Q的左侧()求P，Q两点的坐标；()设直线y2xm(m0)与抛物线的交点为M，N，求证：直线PM，QN，CD交于一点答案解：(1)由题意抛物线的顶点A(2，1)，可以假设抛物线的解析式为ya(x2)21，抛物线经过B(0，)，4a1，a抛物线的解析式为y(x2)21(2)证明：过点P作PJAF于JP(m，n)，n(m2)21m2m，P(m，m2m)，dm2m(3)m2m，F(2，1)，PF，d2m4m3m2m，PF2m4m3m2m，d2PF2，PFd(3)如图，过点Q作QH直线l于H，过点D作DN直线l于NDFQ的周长DFDQFQ，DF是定值2，DQQF的值最小时，DFQ的周长最小，由(2)可知QFQH，DQQFDQQH，根据垂线段最短可知，当D，Q，H共线时，DQQH的值最小，此时点H与N重合，点Q在线段DN上，DQQH的最小值为6，DFQ的周长的最小值为26，此时Q(4，)解：(1)把A(1，0)和点B(0，3)代入yx2bxc，得，解得：，抛物线解析式为yx22x3；(2)y(x1)24，C(1，4)，抛物线的对称轴为直线x1，如图，设CDt，则D(1，4t)，线段DC绕点D按顺时针方向旋转90，点C落在抛物线上的点P处，PDC90，DPDCt，P(1t，4t)，把P(1t，4t)代入yx22x3得：(1t)22(1t)34t，整理得t2t0，解得：t10(舍去)，t21，P(2，3)；(3)P点坐标为(2，3)，顶点C坐标为(1，4)，将抛物线平移，使其顶点落在原点O，这时点P落在点E的位置，E点坐标为(1，1)，点E关于y轴的对称点F(1，1)，连接PF交y轴于M，则MPMEMPMFPF的值最小，设直线PF的解析式为ykxn，解得：，直线PF的解析式为yx，点M的坐标为(0，)解：(1)点A(1，0)、点B(0，3)，在抛物线上，解得：，所求的抛物线解析式为y=x2+4x+3；(2)设平移后抛物线的解析式为y=x2+4x+3+k它经过点(5，6)，6=(5)2+4(5)+3+kk=2平移后抛物线的解析式为y=x2+4x+32=x2+4x+1配方，得y=(x+2)23a=10，平移后的抛物线的最小值是3(3)由(2)可知，BD=PQ=2，对称轴为x=2又SMBD=2SMPQ，BD边上的高是PQ边上的高的2倍设M点坐标为(m，n)当M点的对称轴的左侧时，则有0m=2(2m)m=4n=(4)2+4(4)+1=1M(4，1)当M点在对称轴与y轴之间时，则有0m=2m(2)m=n=()2+()+1=2M(，2)当M点在y轴的右侧时，则有m=2(m(2)m=40，不合题意，应舍去综合上述，得所求的M点的坐标是(4，1)或(，2)解：(1)将点B、C的坐标代入抛物线表达式得：，解得，故抛物线的解析式为yx22x3；yx22x3(x1)24，D(1，4)；(2)如图B(3，0)，C(0，3)，D(1，4)，BC2323218，BC3，CD212(43)22，CD，BD242(31)220，BD2，BD2BC2CD2，BCD是直角三角形，BCD90，tanCBD；(3)点C关于抛物线yx22x3对称轴的对称点为E点，yx22x3的对称轴为x1，E(2，3)，B(3，0)，直线BE为y3x9，M(1，6)，由(2)知CDB是直角三角形，BCD90，若CDB和BMP相似，可分两种情况进行解析：MPBBCD90时，点P在x轴上，M(1，6)，B(3，0)，PM6，BP2，MPBBCD90，CDB和PBM，P(1，0)；MBPBCD90时，M(1，6)，B(3，0)，MB2，CDB和BPM，解得PM，点MP的纵坐标为6，P(1，)综上所述，存在，点P的坐标为(1，0)或(1，)解：(1)抛物线yx2bxc的顶点D坐标为(1，4)，y(x1)24x22x14x22x3，抛物线解析式为yx22x3；(2)当y0时，x22x30，解得x11，x23，则A(1，0)，B(3，0)，1m3，设E点的横坐标为t，m11t，t2m，点E的横坐标为2m；故答案为：2m；设F(m，m22m3)(1m3)，则E(2m，m22m3)，矩形EFGH为正方形，FGFE，即m22m3m(2m)，整理得m25，解得m1(舍去)，m2，G点坐标为(，0)；过点D作DMx轴于M，EGAD，而DMx轴，14，RtGEHRtDAM，即GH2EH，即2m22(m22m3)，整理得m2m40，解得m1(舍去)，m2，G点坐标为(，0)；(3)设AD交EF于Q，如图，FPAD，DPF90，DFP与DAM相似13，12，23，而FPDQ，FDQ为等腰三角形，FDFQ，设直线AD的解析式为ypxq，把A(1，0)，D(1，4