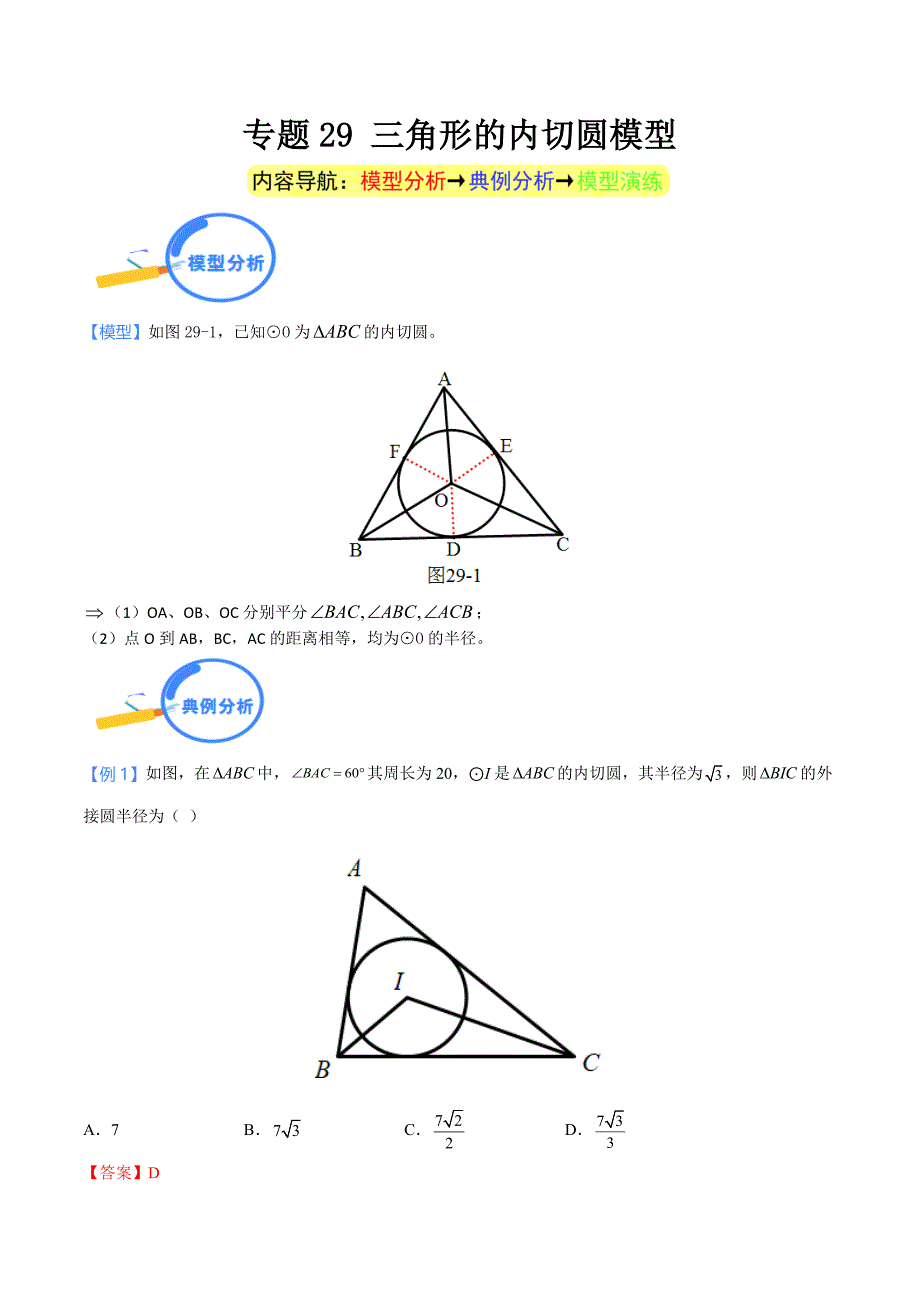
专题29 三角形的内切圆模型【模型】如图29-1，已知O为的内切圆。（1）OA、OB、OC分别平分；（2）点O到AB，BC，AC的距离相等，均为O的半径。【例1】如图，在中，其周长为20，I是的内切圆，其半径为，则的外接圆半径为（ ）A7BCD【答案】D【分析】过C作CDAB于D，由结合面积求出BC的长，由内心可以求出，的外接圆圆心为O,F是优弧BC上任意一点，过O作OEBC于E，求出圆心角，最后由垂径定理求出半径OB【解析】过C作CDAB于D，的外接圆圆心为O,F是优弧BC上任意一点，过O作OEBC于E，设，在周长为20，内切圆半径为，中，在周长为20，解得是的内心BI、CI分别平分ABC、ACBOEBC,故选D【例2】如图，中，则的内切圆半径为_【答案】4【分析】先作ADBC于点D，利用勾股定理求AD，再求三角形ABC的面积，利用内心与三顶点连线将三角形分成三个三角形，利用内切圆的半径求三个三角形面积，利用面积构造r的等式，求出即可【解析】过A作ADBC于点D，设BD=x，CD=14-x，AD2=AB2-BD2=AC2-CD2，132-x2=152-(14-x)2，解得：x=5，AD=，SABC=84，设的内切圆半径为r，连结AI，BI，CI，则，SABC=，21r=84，r=4，故答案为：4【例3】如图，AB=AC，CDAB于点D，点O是BAC的平分线上一点，O与AB相切于点M，与CD相切于点N（1）求证：AOC=135；（2）若NC=3，BC=，求DM的长【答案】（1）见解析；（2）DM=1【分析】(1)只要证明OC平分ACD，即可解决问题；(2)由切线长定理可知：AM=AE，DM=DN，CN=CE=3，设DM=DN=x，在RtBDC中，根据，构建方程即可解决问题【解析】（1）证明：连接OM，ON，过O点做OEAC，交AC于E，如图所示，O与AB相切于点M，与CD相切于点NOMAB，ONCD，OA平分BAC，OEAC，OMAB，OM=OE，即：E为O的切点；OE=ON，又OEAC，ONCD，OC平分ACD，CDAB，ADC=90，DAC+ACD=90，OAC+OCA=45，AOC=180-（OAC+OCA）=180-45=135，即：AOC=135，（2）由（1）得，AM=AE，DM=DN，CN=CE=3，设DM=DN=x，AB=AC，BD=AB-AD=AC-AE-DM=CE=DM=3-x，CD=3+x，在RtBCD中，由勾股定理得：，即：，解得：x=1或x=-1（舍去），即DM=1一、单选题1若的外接圆半径为R，内切圆半径为，则其内切圆的面积与的面积比为（）ABCD【答案】B【分析】画好符合题意的图形，由切线长定理可得：结合勾股定理可得：再求解直角三角形的面积，从而可得直角三角形的内切圆的面积与直角三角形的面积之比【解析】解：如图，由题意得： ，由切线长定理可得： 设， ， 而 故选B2如图，O是等边ABC的内切圆，分别切AB，BC，AC于点E，F，D，P是上一点，则EPF的度数是（）A65B60C58D50【答案】B【分析】连接OE，OF求出EOF的度数即可解决问题【解析】解：如图，连接OE，OFO是ABC的内切圆，E，F是切点，OEAB，OFBC，OEB=OFB=90，ABC是等边三角形，B=60，EOF=120，EPF=EOF=60，故选：B3如图，已知矩形的周长为，和分别为和的内切圆，连接，若，则的长为（）ABCD【答案】B【分析】设AB=x，BC=y，内切圆半径为r，由矩形的对称性知，结合直角三角形内切圆半径与三角形面积间的关系得到x、y、r的关系式，再由推导出x、y、r的关系，从而分别求出r，xy、的值，最后由勾股定理求得EF值.【解析】如图，设AB=x，BC=y，内切圆半径为r，则AC=矩形的周长为，x+y=8和分别为和的内切圆，由矩形的对称性知，即由、联立方程组，解得：r=1，xy=14，作EHFH于H，由勾股定理得：=36-32+8=12，EF=，故选：B.4如图，点是的内心，则 ()ABCD【答案】D【分析】根据三角形内角和定理求出，求出，求出的度数，根据三角形的内角和定理求出即可【解析】解：，点是的内心，故选：D二、填空题5已知平面直角坐标系中，点A(5，0)、B(，)和点P(a，a)若M是PAB的内切圆，则M面积的最大值是_【答案】【分析】先求出AB解析式，得到AB与l平行，求出SABP为定值，由SABP=，可得当PAB的周长最小时符合题意，再根据对称性得到PAB的周长值求出r，故可求解【解析】设直线AB的解析式为y=kx+b把A(5，0)、B(，)代入得解得P(a，a)P点在直线l：上ABlSABP为定值如图，作ACl，在RtAOC中，k=tanAOC设AC=3a，CO=4a，AO=5，AC2+CO2=AO2，即（3a）2+（4a）2=52，解得a=1，AC=3，AB=，SABP=为定值，设PAB的内切圆M半径为r，SABP= ，当最小时，=AB+BP+AP，当BP+AP最小时符合题意，作点A关于直线l的对称点D，PD=PA，当PA+PB=BD时，BP+AP最小，ABl，DAB=90，AD=2AC=6，BD=，最小值为18，此时r=，M面积为=，故答案为：6如图，在中，为的内切圆，与分别交于点，则劣弧的长是_【答案】【分析】先利用勾股定理计算出，再利用直角三角形内切圆半径的计算方法得到，接着三角形角平分线的性质得到，然后根据弧长公式计算劣弧的长【解析】解：，为的内切圆，平分，平分，劣弧的长故答案为7如图所示的网格由边长为个单位长度的小正方形组成，点、在直角坐标系中的坐标分别为，则内心的坐标为_【答案】（2，3）【分析】根据A、B、C三点的坐标建立如图所示的坐标系，计算出ABC各边的长度，易得该三角形是直角三角形，设BC的关系式为：y=kx+b，求出BC与x轴的交点G的坐标，证出点A与点G关于BD对称，射线BD是ABC的平分线，三角形的内心在BD上，设点M为三角形的内心，内切圆的半径为r，在BD上找一点M，过点M作MEAB，过点M作MFAC，且ME=MF=r，求出r的值，在BEM中，利用勾股定理求出BM的值，即可得到点M的坐标【解析】解：根据A、B、C三点的坐标建立如图所示的坐标系，根据题意可得：AB=，AC=，BC=，BAC=90，设BC的关系式为：y=kx+b，代入B，C，可得，解得：，BC：，当y=0时，x=3，即G（3,0），点A与点G关于BD对称，射线BD是ABC的平分线，设点M为三角形的内心，内切圆的半径为r，在BD上找一点M，过点M作MEAB，过点M作MFAC，且ME=MF=r，BAC=90，四边形MEAF为正方形，SABC=，解得：，即AE=EM=，BE=，BM=，B（-3，3），M（2，3），故答案为：（2，3）8已知的三边a、b、c满足，则的内切圆半径=_【答案】1【分析】先将变形成，然后根据非负性的性质求得a、b、c的值，再运用勾股定理逆定理说明ABC是直角三角形，最后根据直角三角形的内切圆半径等于两直角边的和与斜边差的一半解答即可【解析】解：则=0，c-3=0，a-4=0，即a=4，b=5，c=3，42+32=52ABC是直角三角形的内切圆半径=1故答案为19如图，的内切圆与分别相切于点，且，则阴影部分的面积为_ (结果保留)【答案】【分析】先根据勾股定理的逆定理得出是直角三角形，再设的半径为r，根据三角形的面积公式得出r的值，然后根据正方形的判定与性质、扇形的面积公式、三角形的面积公式即可得【解析】是直角三角形，且设的半径为r，则内切圆与分别相切于点即解得又四边形AEOF是矩形，矩形AEOF是正方形则故答案为：10如图，是四边形的内切圆，连接、若，则的度数是_【答案】【分析】如图，设四个切点分别为点，分别连接切点与圆心，可以得到4对全等三角形，进而得到，根据这8个角和为360，1+8=，即可求出=5+4=72【解析】解：设四个切点分别为点，分别连接切点与圆心，则，且，在与中，同理可得：，故答案为：三、解答题11已知：问题一：请用圆规与直尺（无刻度）直接在内作内切圆，（要求清晰地保留尺规作图的痕迹，不要求写画法）问题二：若的周长是24，的面积是24，求的内切圆半径【答案】（1）见解析；（2）r=2【分析】（1）先作B和C的平分线交于点O，再过点O作OHAB于H，然后以点O为圆心，OH为半径作圆即可；（2）连结OA、OB、OC，作ODAB于D，OEBC于E，OFAC于F，根据切线的性质得OD=OE=OF=r，则利用SABC=SAOB+SOBC+SOAC得到rAB+rBC+rAC=24，变形得到 r（AB+BC+AC）=24，然后把周长为24代入计算即可得到r的值【解析】解：（1）如图，为所求作的的内切圆；（2）解：如下图，连结OA、OB、OC，作ODAB于D，OEBC于E，OFAC于F，设它的内切圆的半径为r，则OD=OE=OF=r，SABC=SAOB+SOBC+SOAC，rAB+rBC+rAC=24， r（AB+BC+AC）=24， r24=24，r=2即的内切圆的半径为212如图，O是ABC的内切圆，且O与ABC的三边分别切于点D、E、F，已知AB长为10cm，BC长为6cm，AC长为8cm（1）求AE、CD、BF的长；（2）连接OD，OE，判断四边形ODCE的形状，并说明理由；（3）求O的面积【答案】（1）AE=6cm；CD=2c